[수학 1 실전 개념] 6강 : 지수/로그 함수 그래프 (1) - 점근선&정점

안녕하세요,
필수 유형에 대한
실전 개념 정리 입니다~
질문 사항은
아래 오픈챗 링크 혹은 메일로 보내주시면,
2시간 이내로 답변드리겠습니다.
오픈챗 링크 : https://open.kakao.com/o/srASNxef
메일 주소 : studying.all.night.1114@gmail.com
0. 대표 문제

사실, 지금 배우고 있는 수학 1의 1단원은 지수/로그 "함수" 이기에
함수의 그래프를 정확하고 빠르게 그릴 줄 알아야 문제를 쉽게 해결할 수 있습니다.
위 4가지 문제의 그래프를 각각 1분이내로 그려냈다면 아래 글을 읽어보실 필요 없고,
바로 7강으로 넘어가면 되지만, 오래걸렸거나 그래프 그리는 것이 어려우시면
무조건!! 이 글을 정독하고 여러번 다시 그려보아야 합니다.
1. 그래프 그리기 개론
지수/로그 함수의 그래프를 그리는 방법은 정해져 있습니다.
아래의 순서를 따르면 되는데요,

예를 들어 우리가 너무나 잘 알고있는 다음 그래프들을
위 4단계를 적용하여 그릴 수 있습니다

먼저 아래와 같이 점근선을 그릴 수 있습니다.

위 그래프(y=2^x)의 점근선이 x축임은 잘 알려져 있습니다.
(점근선을 구하는 자세한 내용은 뒤에 다룹니다)
점근선을 구했다면, 이제 증가 감소를 파악해야 합니다.

점근선과 마찬가지로, 밑>1 이므로 증가함수 인것이 알려져 있습니다.
(증가/감소를 구하는 자세한 내용 또한 뒤에서 다룹니다)
마지막으로 정점 또는 절편을 하나 찾으면 됩니다.
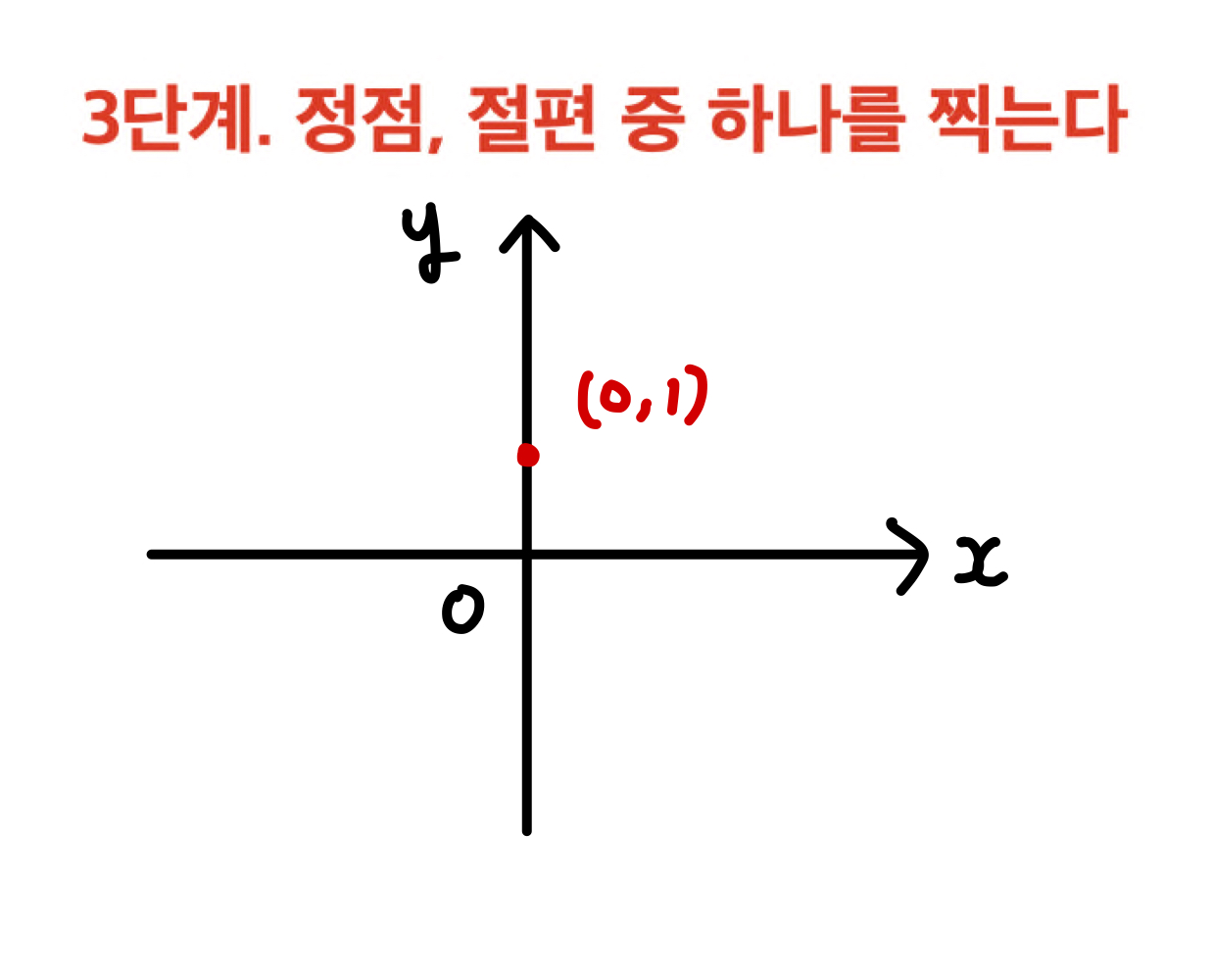
1, 2, 3단계를 완료 했다면, 이를 종합하여 그래프를 그리면 끝입니다!
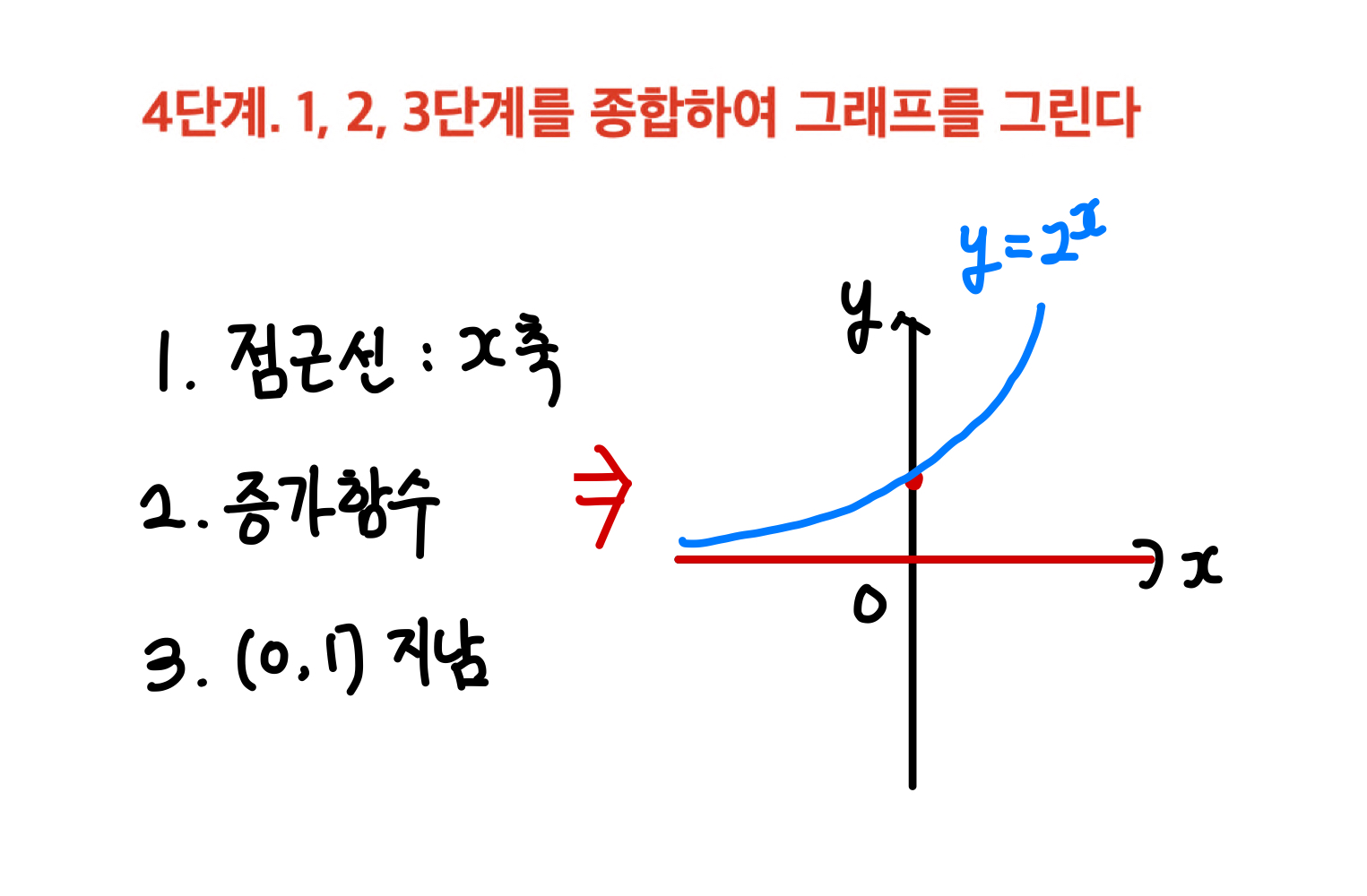
위의 1, 2, 3, 4단계를 거치면 모든 지수/로그 함수를 빠르고 정확하게 그릴 수 있습니다.
이제 단계별로 점근선, 증가/감소, 정점/절편을 확실하게 파악하는 방법론을 알아보겠습니다.
2. 점근선 빠르게 구하기
(1) 지수함수의 점근선
지수함수의 점근선은 아래와 같은 일반적인 지수함수 그래프에서

맨 뒤만 신경써주면 됩니다.
즉, 다음과 같이 y = e가 점근선이 되는 것이죠
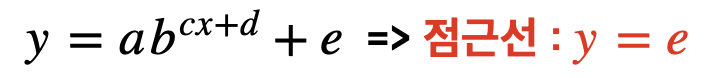
그렇다면 왜 y=e가 점근선이 되는 것일까요?
이는, 평행이동의 관점에서 해석할 수 있으며 다음과 같은 사실을 받아들이고 갑시다.

그러므로, 점근선이 y=0 (x축인) 다음 지수함수를 평행이동할 경우
점근선 또한 함께 평행이동 됩니다
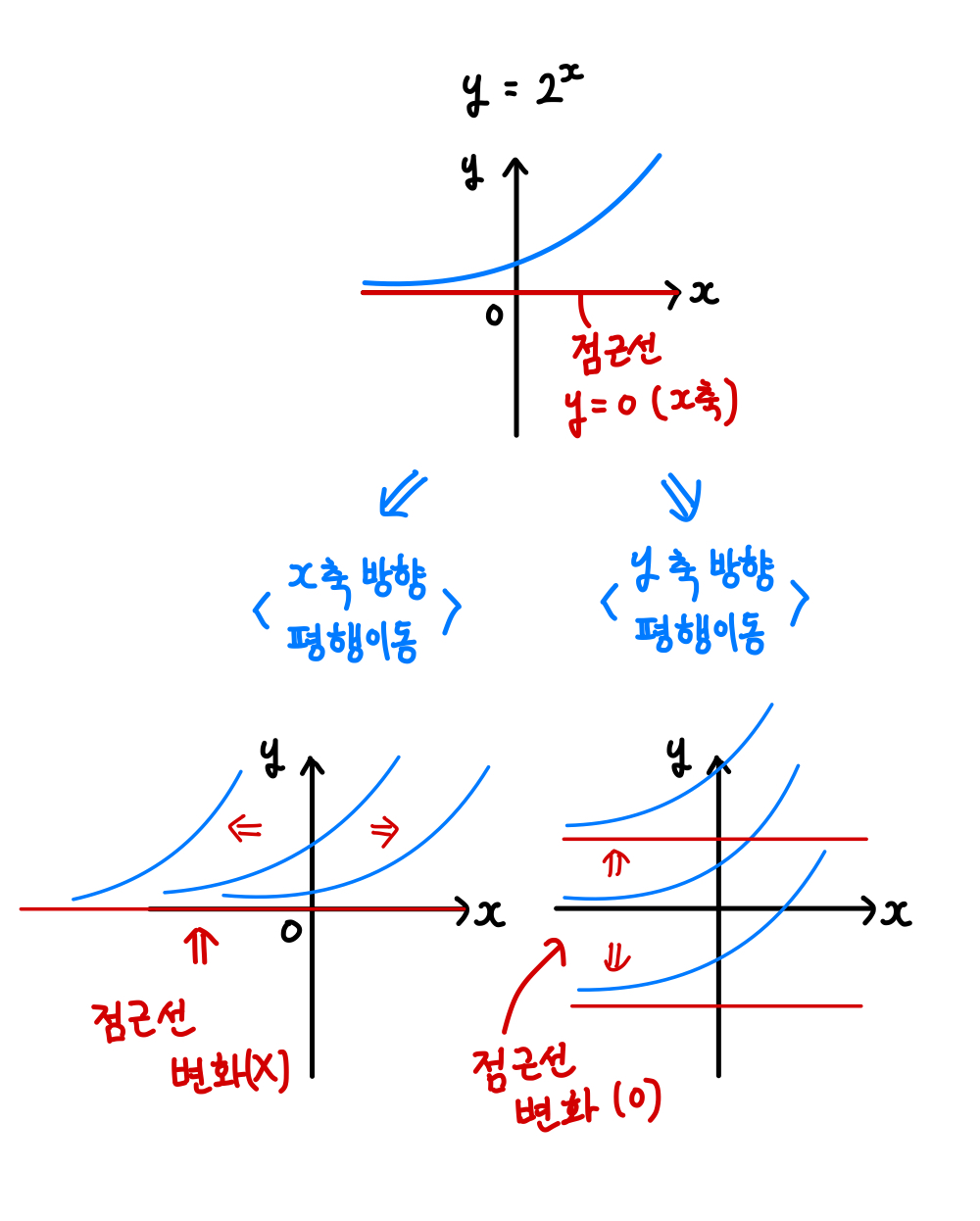
위 그림을 보면 알 수 있듯이,
x축으로 평행이동 -> 점근선 변화 (x)
y축으로 평행이동 -> 점근선 변화 (o)
사실, 애초에 점근선이 y = 0 (x축) - 가로선 이었기에
x축으로의 평행이동 - 가로방향 은 영향을 줄 수 없고,
y축으로의 평행이동 - 세로방향 은 영향을 주는 것입니다.
따라서, 지수함수의 경우
y축 방향으로의 평행이동이 점근선의 변화를 가져옴을 알 수 있고,
아래와 같은 식에서 점근선을 결정할 수 있습니다.

마지막으로 아래 함수들의 점근선을 구해볼까요?

스스로 먼저 생각해보고 (특히, 예4와 예5)
아래 답을 보면 좋을 것 같습니다~
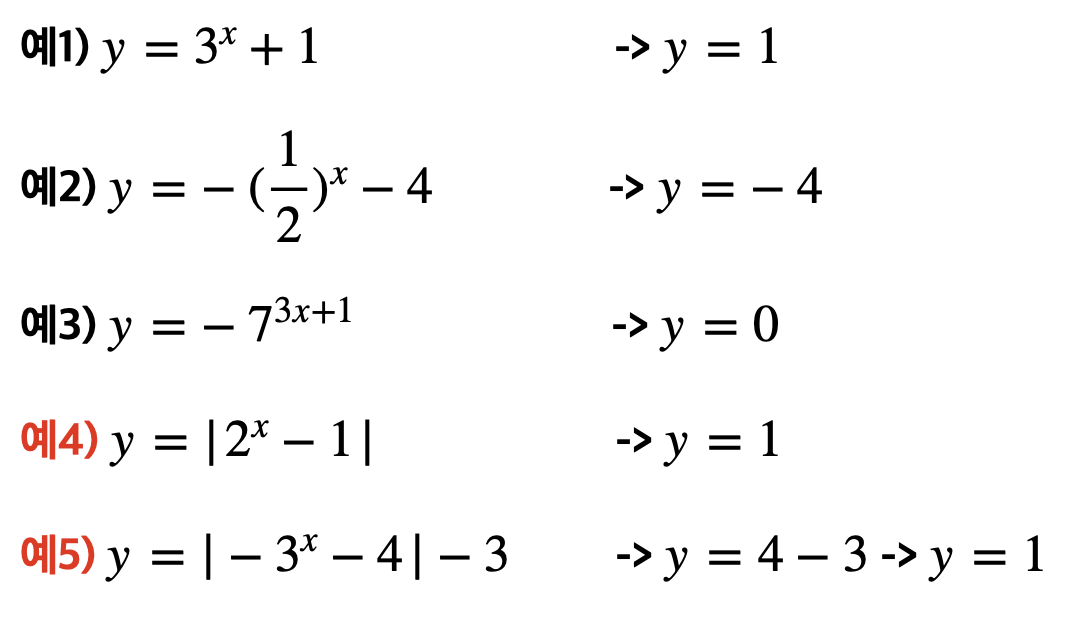
예4)에 대한 첨언
절댓값이 없다면, y = -1 이 점근선일 테지만
절댓값으로 인하여 음수인 값은 양수가 되므로 y = 1 이 점근선이 됩니다.
예5)에 대한 첨언
예4)로 인하여 절댓값 부분의 점근선은 y=4 임을 알 수 있습니다.
이후 y축의 방향으로 -3만큼 평행이동했으므로 점근선 또한 y=1 이 됩니다
(2) 로그함수의 점근선
글을 쓰다보니 좀 길어진 감이 있지만,
해당 내용은 지수/로그 함수의 중추가 되는 부분이라 그런지
상세히 쓰게 되네요 ㅎㅎ..
로그함수의 점근선은 아래와 같은 일반적인 로그함수 그래프에서
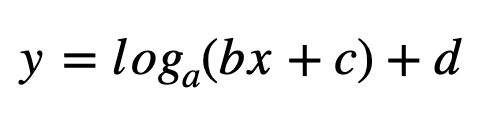
진수부분만 신경써주면 됩니다.
즉, 다음과 같이 x = -c/b 가 점근선이 되는 것이죠

그렇다면 왜 x = -c/b가 로그함수의 점근선이 되는 것일까요?
지수함수와 마찬가지로, 평행이동의 관점에서 해석할 수 있습니다.
그러므로, 점근선이 x=0 (y축인) 다음 로그함수를 평행이동할 경우
점근선 또한 함께 평행이동 됩니다 (다만, 지수/로그 함수는 서로 역함수 관계이므로
경향성이 반대이지 않을까 하는 추측을 해볼 수 있습니다.)

위 그림을 보면 알 수 있듯이,
x축으로 평행이동 -> 점근선 변화 (o)
y축으로 평행이동 -> 점근선 변화 (x)
사실, 애초에 점근선이 x = 0 (y축) - 세로선 이었기에
x축으로의 평행이동 - 가로방향 은 영향을 줄 수 있고,
y축으로의 평행이동 - 세로방향 은 영향을 줄 수 없는 것입니다.
따라서, 로그함수의 경우
x축 방향으로의 평행이동이 점근선의 변화를 가져옴을 알 수 있고,
아래와 같은 식에서 점근선을 결정할 수 있습니다.

마지막으로 아래 로그 함수들의 점근선을 구해볼까요?
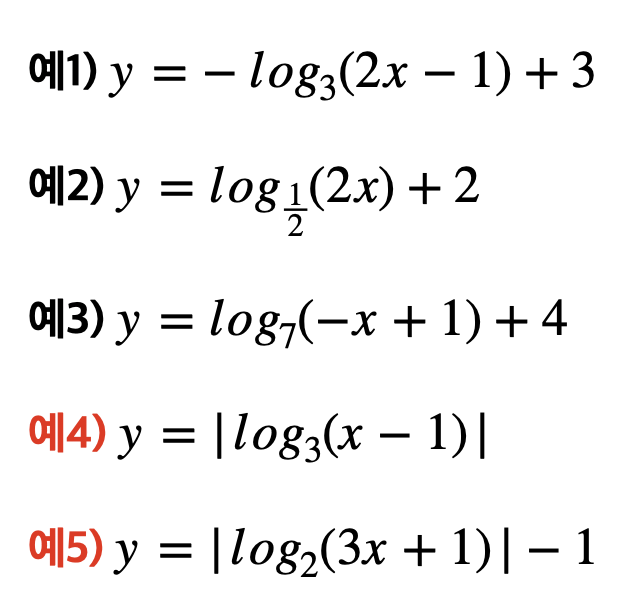
스스로 먼저 생각해보고 (특히, 예4와 예5)
아래 답을 보면 좋을 것 같습니다~

정리를 좀 하면, 말만 거창하지
로그 함수의 점근선 -> x = 진수가 0이 될 때!
지수 함수의 점근선 -> y = 지수식 뒷 부분!
임을 이해하고 계시면 됩니다~
3. 증가/감소 빠르게 판단하기
(1) 기본 형태
증가 감소는 기본적으로 지수/로그 함수 모두 밑이 1보다 크냐 작냐로 판단할 수 있습니다.
즉, 밑이 1보다 클 때는 다음과 같이 지수/로그 모두 증가함수가 됩니다

반면, 밑이 1보다 작을 때는 다음과 같이 지수/로그 모두 감소함수가 됩니다
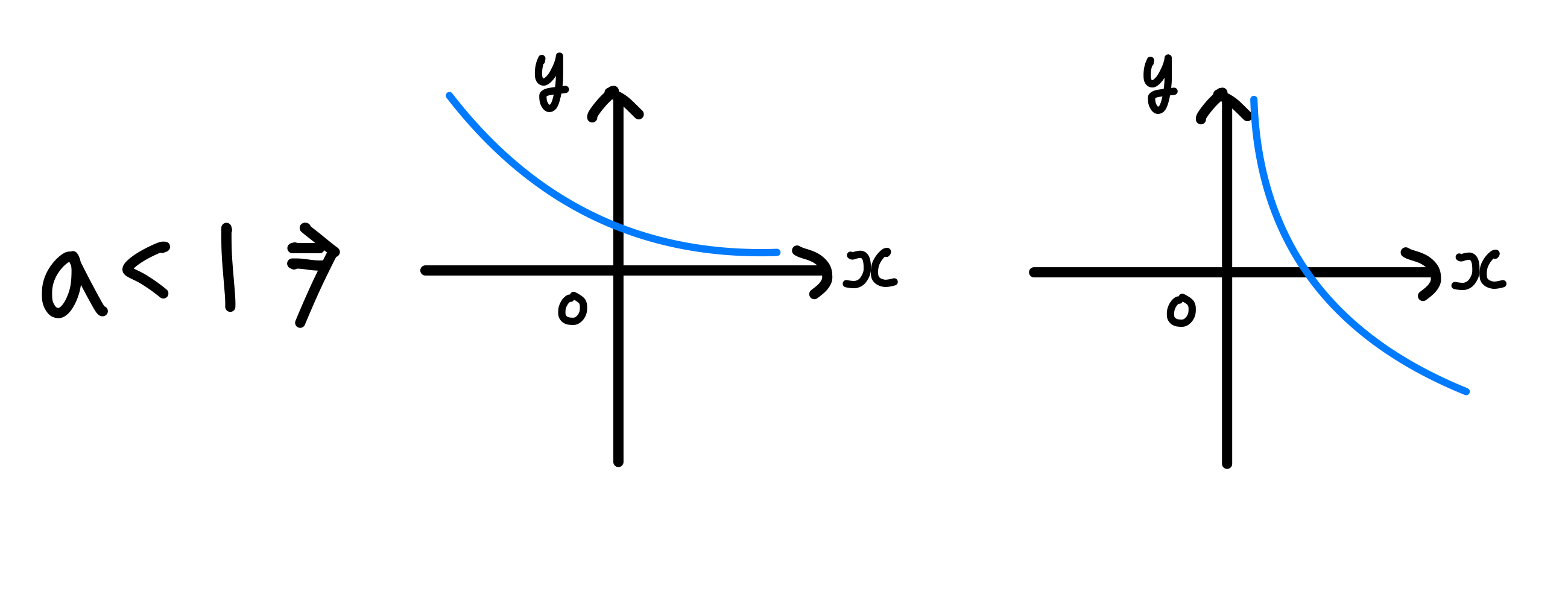
그러므로, 다음 예시의 증감을 판단해보면

예1)의 경우 밑이 1보다 작으므로, 감소함수 입니다.
(x축과 y축 방향으로의 평행이동은 증가/감소에 영향을 주지 않습니다)
예2)의 경우 밑이 1보다 크므로, 증가함수 입니다
(마찬가지로 x축과 y축 방향으로의 평행이동은 증가/감소에 영향을 주지 않습니다)
그러나, 예3)과 예4)의 경우 평행이동이 아닌, 대칭이동이므로
증가/감소가 바뀌게 됩니다. 이에 대해 아래에서 자세히 다뤄봅시다
(2) 대칭이동된 형태
대칭이동하게 될 경우, 증가/감소가 바뀌게 되는데 다음 예시를 보면 쉽게 알 수 있습니다.


따라서, 1회 대칭이동시 증/감이 반전이 됨을 알 수 있습니다.
그렇다면 함수를 1회가 아닌, 2회 대칭이동하면 어떻게 될까요?
1회 대칭이동시 증/감이 반전 되므로
x축, y축에 대해 동시에 대칭이동하는 경우에는 (= 원점대칭)
증/감이 그대로 유지 됩니다

그러므로, 위의 예시를 해석해보면
예3)의 경우 밑이 1보다 크므로, 기본적으로는 증가함수 입니다.
그러나, y축으로 1회 대칭이동 했으므로 감소함수가 됩니다
예4)의 경우 밑이 1보다 크므로, 기본적으로는 증가함수 입니다
그러나, x축으로 1회 대칭이동 했으므로 감소함수가 됩니다
예5)의 경우 밑이 1보다 작으므로, 기본적으로는 감소함수 입니다
이때, x축으로 1회 대칭이동 + y축으로 1회 대칭이동 했으므로 감소함수로 유지됩니다
4. 정점 찍기
이제, 지수/로그 함수 그리기의 마지막 단계인 정점 찍기에 대해 살펴보도록 하겠습니다
먼저 정점에 대해 살펴보죠
(1) 정점이란
지수/로그 함수에서 정점의 의미는
밑의 값과 관계 없이 항상 지나는 점을 말합니다
(즉, 밑이 100이든 1000이든 지나게 되는 점)

먼저 위와 기본적 지수함수의 경우
정점의 좌표가 (0, 1) 이 됩니다.

위의 3가지 식 모두 밑에 관계 없이 (0, 1)을 지남을 알 수 있는데
그 이유는, (밑)의 값이 무엇이 되더라도 (지수)가 0이라면 값 자체가 1이 되기 때문입니다

그렇다면 평행이동과 대칭이동이 된
위의 지수함수에서 정점은 무엇이 될까요?
정점은 밑의 값에 관계없이 항상 지나는 점이라고 했으니
a의 값과 관계가 없이 위해서는
bx+c = 0 이 될때
a가 100이든, 1000이든 y = 1+d 가 됨을 알 수 있습니다
예를 들어보면 다음과 같죠

또한, 로그함수의 경우는 다음과 같이 정리할 수 있습니다.
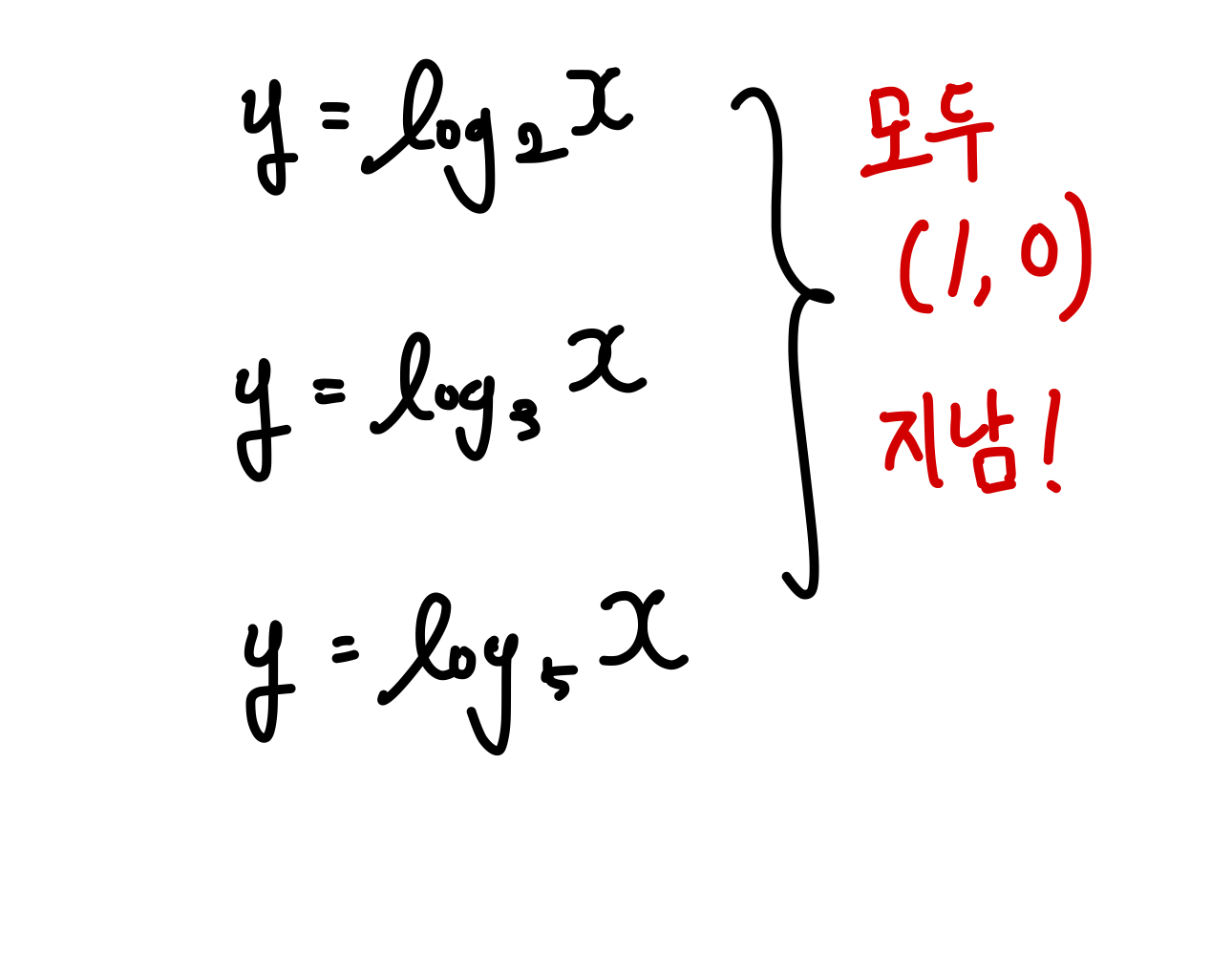
지수함수의 경우 -> 정점 : (지수) = 0 일때
로그함수의 경우 -> 정점 : (진수) = 1 일때
(2) 다양한 지수/로그 함수의 정점 예시
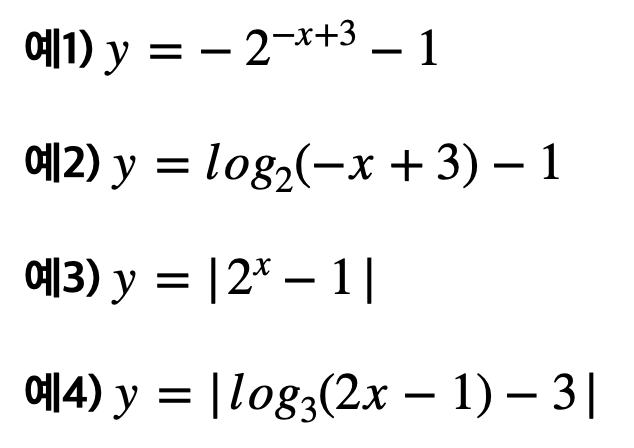
예1) 지수함수의 정점 -> (지수) = 0 일때 이므로,
x=3 일때 -> y = -2
예2) 로그함수의 정점 -> (진수) = 1 일때 이므로,
x=2 일때 -> y = -1
예1) 지수함수의 정점 -> (지수) = 0 일때 이므로,
x=0 일때 -> y = 0 (절댓값은 함숫값에만 영향을 줌)
예1) 로수함수의 정점 -> (진수) = 1 일때 이므로,
x=1 일때 -> y = 3 (절댓값은 함숫값에만 영향을 줌)
5. 총정리

이제 맨 처음에 봤던 그래프를 그린 뒤 마무리하면 될 것 같습니다~
6. 문제 해설


< 사고 흐름 >
점근선 y = 1 을 먼저 좌표 평면 위에 표시하고
밑>1 에서 x축으로 1회 대칭이동 했으니 감소함수임을
체크해 두고
(지수) = 0 일 때, 정점 (1, 0)을 찍습니다
방금 찍은 정점에서 점근선에 가까이 가되 감소하도록
그리면 됩니다
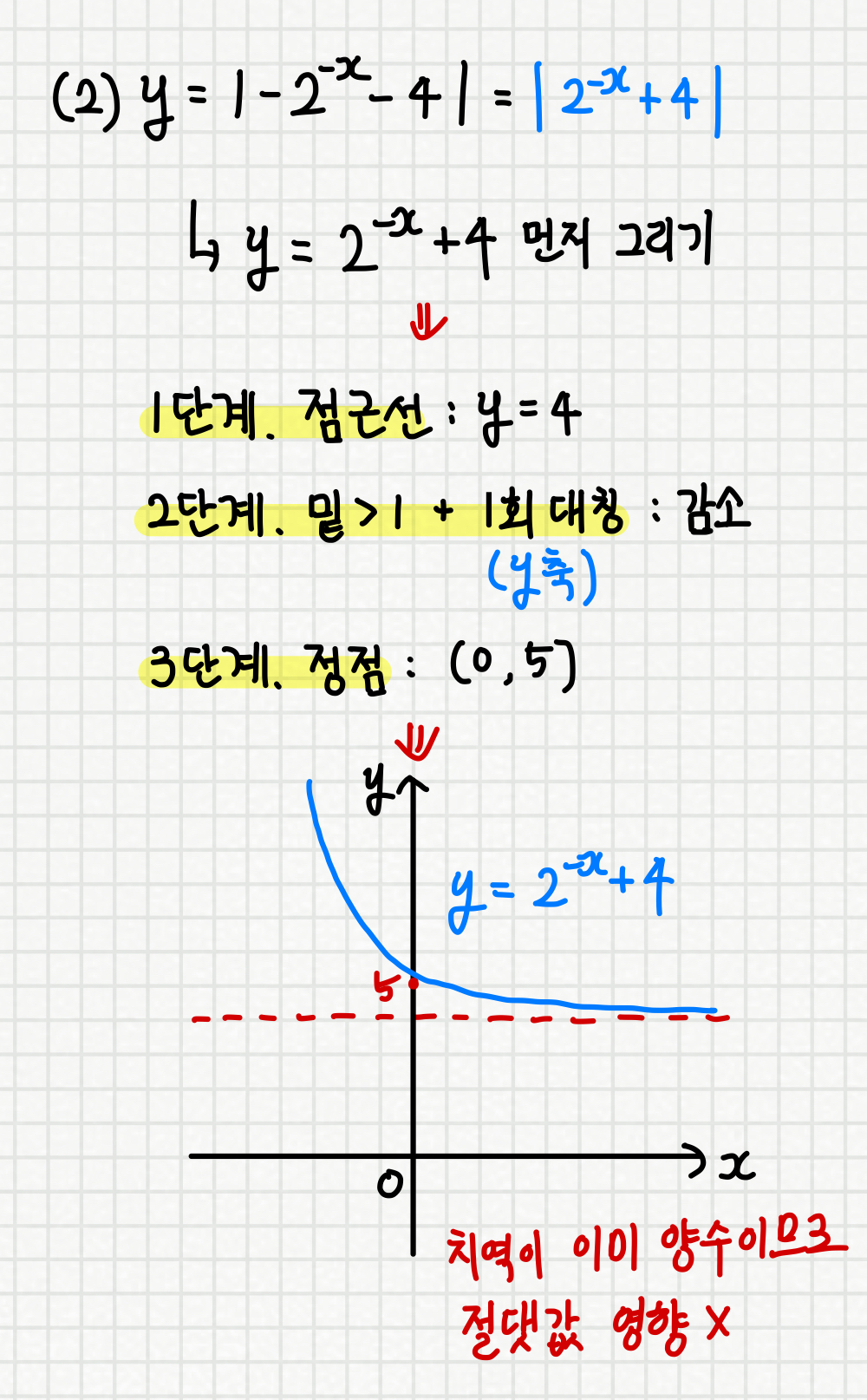
< 사고 흐름 >
절댓값 안쪽을 먼저 그린 후 마지막에 절댓값을 다시 씌우면 됩니다
점근선 y = 4 을 먼저 좌표 평면 위에 표시하고
밑>1 에서 y축으로 1회 대칭이동 했으니 감소함수임을
체크해 두고
(지수) = 0 일 때, 정점 (0, 5)을 찍습니다
방금 찍은 정점에서 점근선에 가까이 가되 감소하도록
그리면 됩니다
마지막으로 점근선 체크시,
좌측 함수의 경우 이미 치역(y값)이 양수이므로
절댓값의 영향이 없습니다

< 사고 흐름 >
점근선 x = 0 을 먼저 좌표 평면 위에 표시하고
밑>1 에서 2회 대칭이동 했으니 증가함수임을
체크해 두고
(진수) = 1 일 때, 정점 (-1/4, 1)을 찍습니다
방금 찍은 정점에서 점근선에 가까이 가되 증가하도록
그리면 됩니다

< 사고 흐름 >
먼저 절댓값 안의 그래프를 그린 뒤,
마지막에 절댓값을 씌워 주도록 합시다.
점근선 x = -1/2 을 먼저 좌표 평면 위에 표시하고
밑>1 에서 증가함수임을
체크해 두고
(진수) = 1 일 때, 정점 (0, 0)을 찍습니다
방금 찍은 정점에서 점근선에 가까이 가되 증가하도록
그리면 됩니다
그 뒤, 절댓값을 붙임으로써
y값이 음수인 부분을 양수쪽으로 들어올립니다.
마지막으로, y축의 방향으로 3만큼 평행이동해주면
완벽한 그래프 완성!
후, 오늘 양이 정말 많았네요.
꼭 여러번 읽어보시고!
이해가 안되는 부분은 질문하고 넘어가시기를
당부드립니다
다음 시간에는 <지수/로그 함수 그래프 (2) - 정의역/치역/비율관계>
로 돌아오겠습니다~
'밤샘수학 > 수학1 실전 개념' 카테고리의 다른 글
| [수학 1 실전 개념] 8강 : 지수/로그 함수 그래프 (3) - 역함수 (2) | 2023.03.30 |
|---|---|
| [수학 1 실전 개념] 7강 : 지수/로그 함수 그래프 (2) - 정의역/치역/비율 (0) | 2023.03.29 |
| [수학 1 실전 개념] 5강 : 상수를 도입 하라 (0) | 2023.03.27 |
| [수학 1 실전 개념] 4강 : 지수의 연쇄법칙 (0) | 2023.03.26 |
| [수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고 (0) | 2023.03.25 |
댓글
이 글 공유하기
다른 글
-
[수학 1 실전 개념] 8강 : 지수/로그 함수 그래프 (3) - 역함수
[수학 1 실전 개념] 8강 : 지수/로그 함수 그래프 (3) - 역함수
2023.03.30 -
[수학 1 실전 개념] 7강 : 지수/로그 함수 그래프 (2) - 정의역/치역/비율
[수학 1 실전 개념] 7강 : 지수/로그 함수 그래프 (2) - 정의역/치역/비율
2023.03.29 -
[수학 1 실전 개념] 5강 : 상수를 도입 하라
[수학 1 실전 개념] 5강 : 상수를 도입 하라
2023.03.27 -
[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
2023.03.26