[수학 1 실전 개념] 7강 : 지수/로그 함수 그래프 (2) - 정의역/치역/비율

안녕하세요, 필수 유형에 대한

실전 개념 정리 입니다~

 

질문 사항은

아래 오픈챗 링크 혹은 메일로 보내주시면,

2시간 이내로 답변드리겠습니다.

 

오픈챗 링크 :  https://open.kakao.com/o/srASNxef

메일 주소 : studying.all.night.1114@gmail.com

 

본격적으로 오늘 강의 내용을 들어가기 앞서

앞으로의 목차를 먼저 살펴보도록 하겠습니다~

 

[지수/로그 목차]

위 내용들은 이미 포스팅 했으니

보지 못하신 분들은 먼저 보고 오시기를 당부드립니다~

[지수/로그 함수 목차]

[삼각함수 목차]

대략적으로 4월 중순에 모든 글들이 포스팅 완료될 예정입니다

 

다시 오늘 수업 내용으로 가봅시다

 

0. 대표 문제

 

[정의역의 중요성]

위 4가지 함수의 차이에 대해 명확히 알고 있어야 합니다

풀이는 관련 개념 설명 뒤에 배치해 두었습니다~

 

 

 

 

1. 지수함수의 정의역과 치역

 

(1) 기본 형태

[지수함수의 기본 형태 - 정의]

위와 같은 지수 함수의 정의역과 치역은 다음과 같습니다

6강에서 자세히 다루었던 그래프를 보면

지수함수는 기본적으로 

 

정의역 : 실수전체

치역 : 양의 실수

 

임을 알 수 있습니다

 

 

 

(2) 평행이동과 대칭이동 시

[지수함수의 평행/대칭 이동]

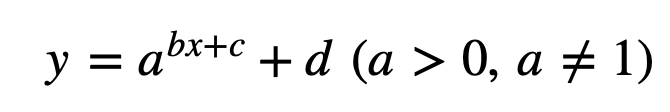
위와 같이 지수함수가 평행이동 및 대칭이동 했을 경우

정의역은 변화가 없습니다. (정의역 : 항상 실수전체)

 

그러나

 

치역의 경우는

1. y축 방향으로의 평행이동 (점근선)

2. x축에 대하여 대칭이동

에 의하여 변하게 됩니다.

 

결론 부터 이야기 하자면

[일반적인 지수함수의 정의역/치역]

6강을 완벽하게 이해하셨다면

위의 내용이 당연한 것으로 받아들일 수 있습니다

 

혹시 몰라 예시 몇 가지를 보면

 

[평행이동만 한 경우]

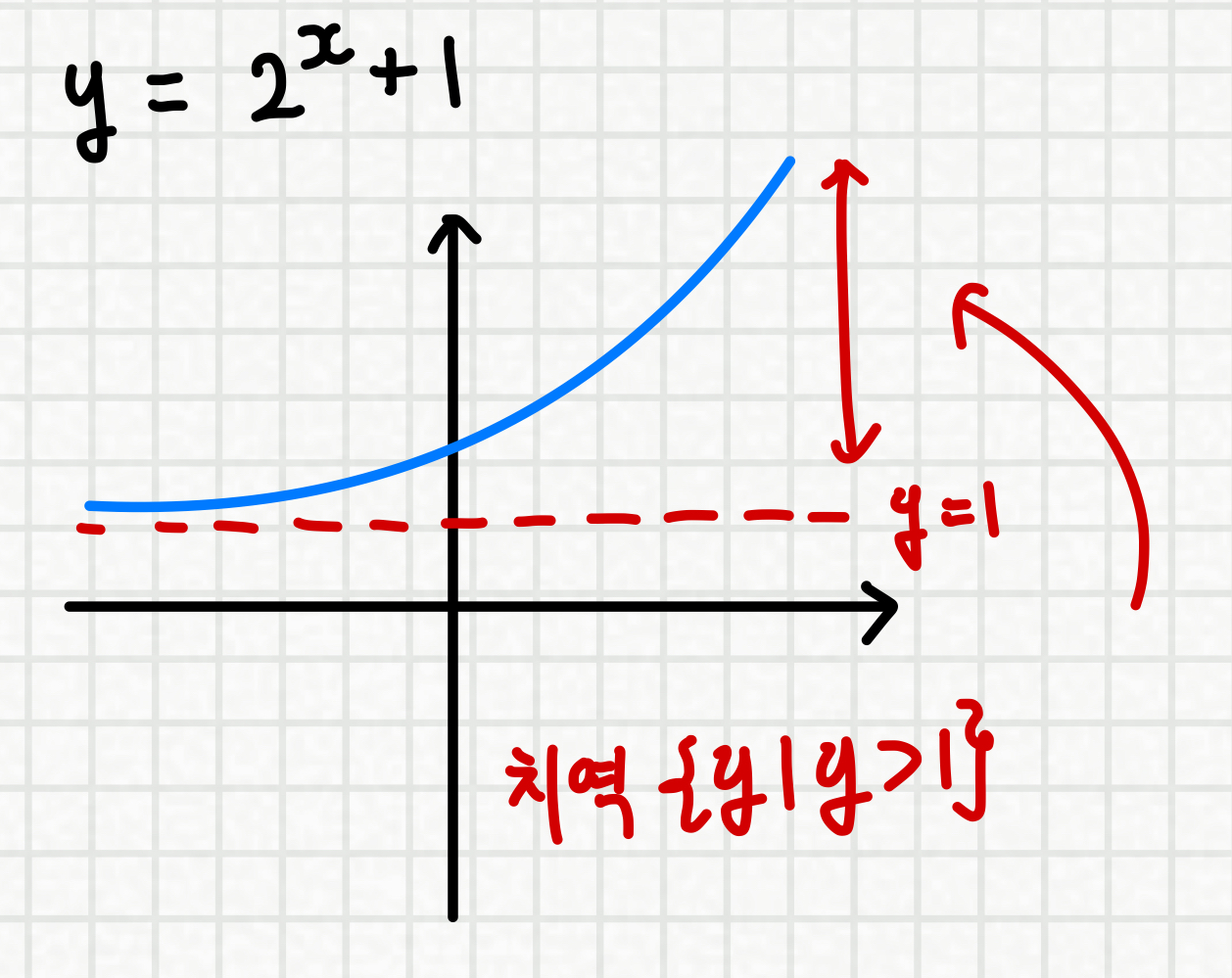
위 그림 처럼  y축 방향으로 평행이동만 했을 경우

(x축 방향으로의 대칭이동은 치역 영향 X)

치역의 부등호 방향은 그대로 이지만

점근선이 변헀으므로

y > 0 -> y > 1 로 값이 변하게 됩니다

 

[x축에 대하여 대칭이동만 한 경우]

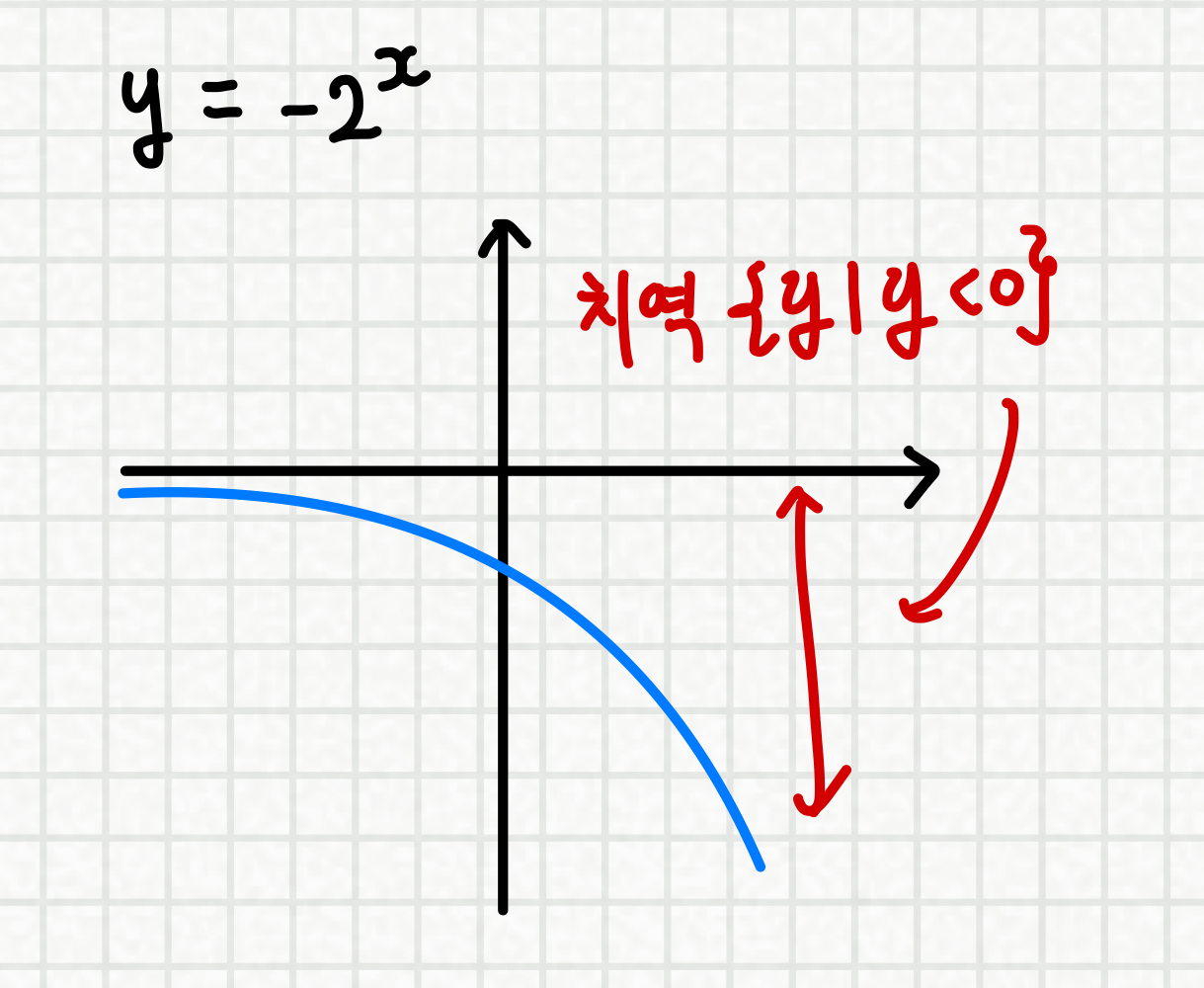
x축에 대하여 대칭이동만 했을 경우

(y축으로의 대칭이동은 치역 영향 X)

치역의 값은 그대로 이지만

y > 0 -> y < 0 으로 부등호 방향이 변하게 됩니다

[평행이동과 대칭이동 모두 한 경우]

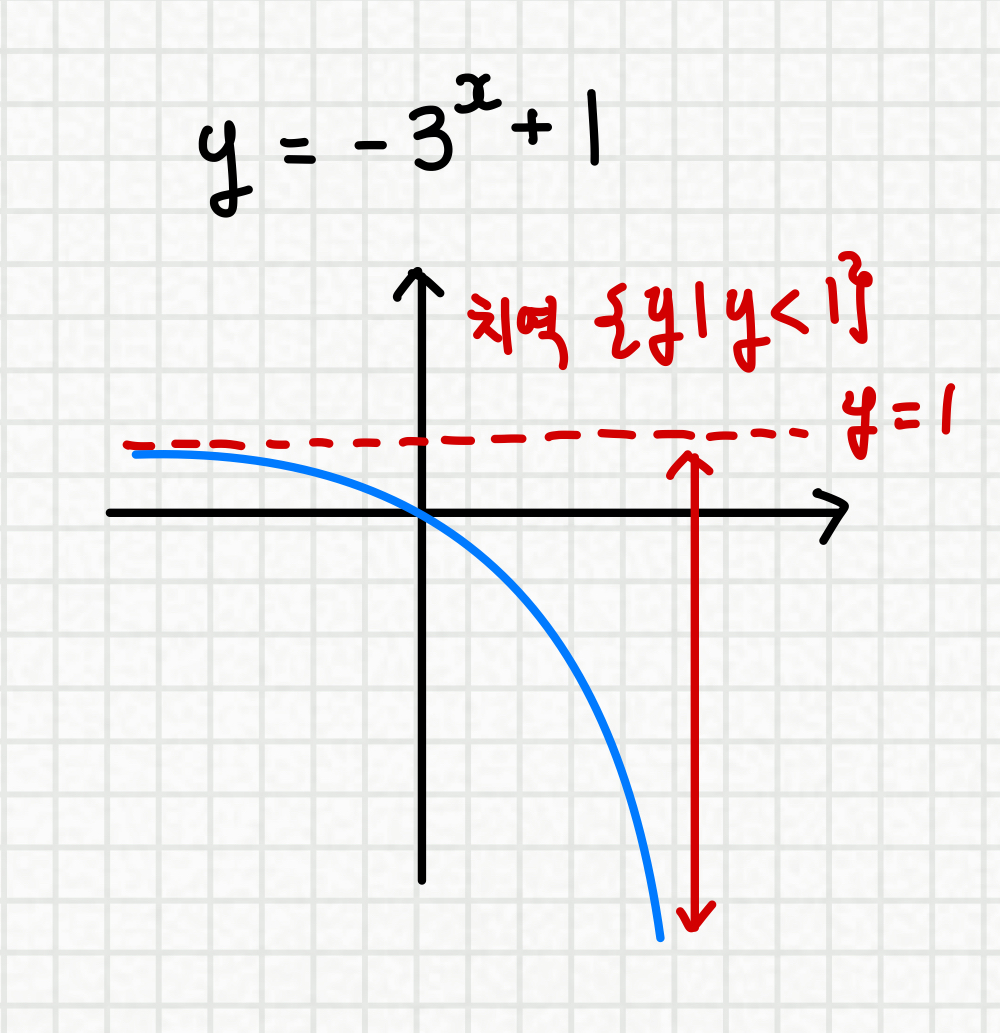
y축 방향으로의 평행이동과

x축에 대하여 대칭이동 했을 경우

 

치역의 값과 부등호 방향 모두 변하게 됩니다

 

 

 

*중요

이때, 우리가 얻어가야 할 점은

나중에 배울 지수/로그 방부등식 - 치환 부분에서

 

지수를 치환할 때 

치환한 문자의 범위는 지수 함수의 치역과 같습니다

 

[지수 방부등식 치환 - 범위1]

[지수 방부등식 치환 - 범위2]

 

 

2. 로그함수의 정의역과 치역

 

(1) 기본 형태

[로그 함수의 기본 형태 - 정의]

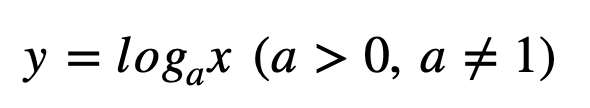
위와 같은 로그 함수의 정의역과 치역은 다음과 같습니다

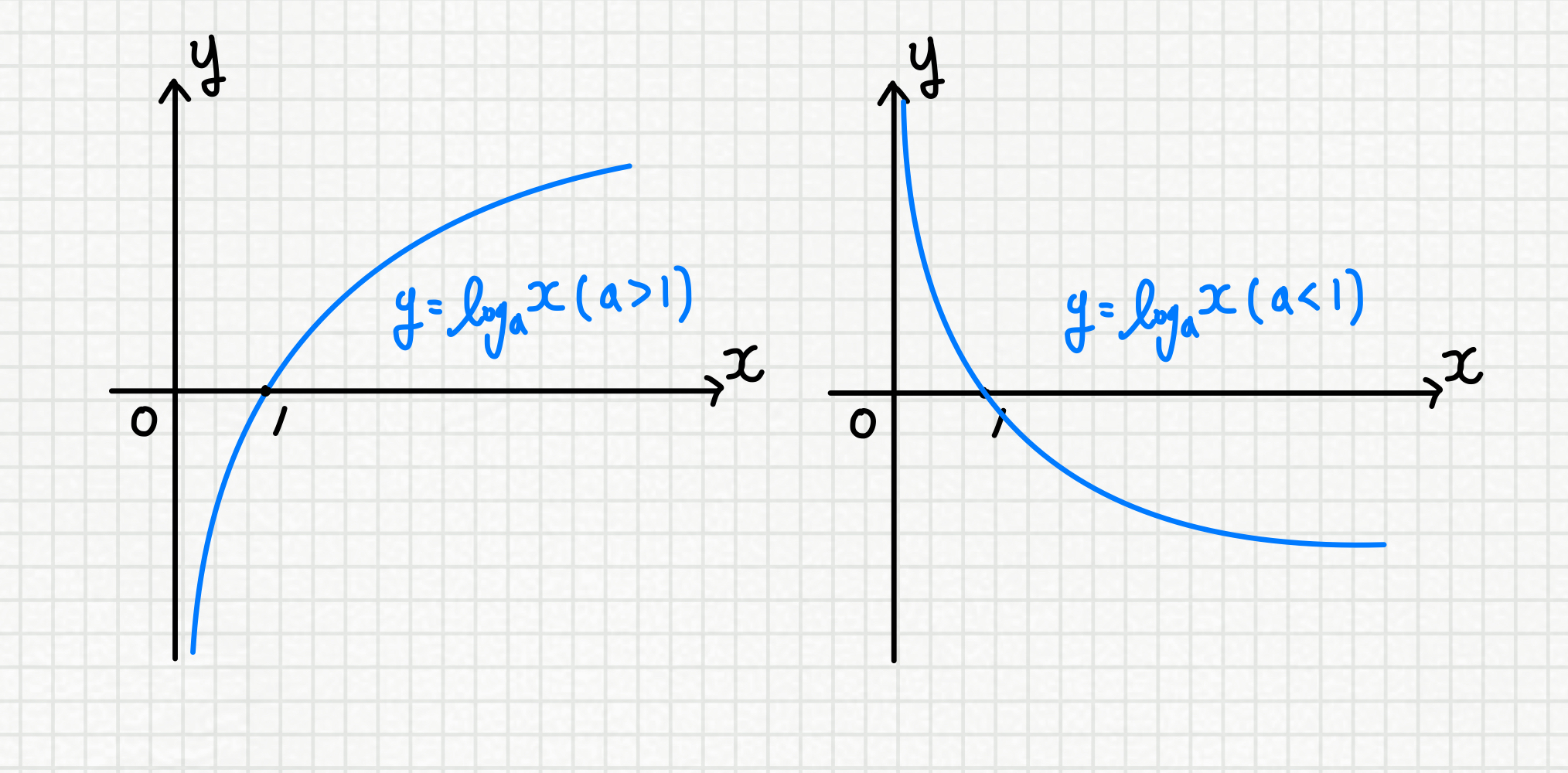
6강에서 자세히 다루었던 그래프를 보면

로그수는 기본적으로 

 

정의역 : 양의 실수

치역 : 실수 전체

 

임을 알 수 있습니다

 

 

 

(2) 평행이동과 대칭이동 시

[로그함수의 평행/대칭 이동]

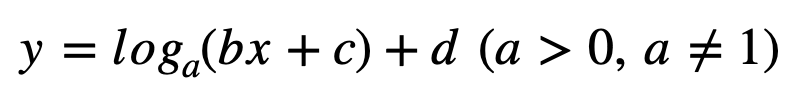
위와 같이 로그함수가 평행이동 및 대칭이동 했을 경우

치역은 변화가 없습니다. (치역 : 항상 실수전체)

 

그러나

 

정의역의 경우는

1. x축 방향으로의 평행이동 (점근선)

2. y축에 대하여 대칭이동

에 의하여 변하게 됩니다.

 

결론 부터 이야기 하자면

[일반적인 로그함수의 정의역/치역]

6강을 완벽하게 이해하셨다면

위의 내용이 당연한 것으로 받아들일 수 있습니다

 

혹시 몰라 예시 몇 가지를 보면

 

[평행이동만 한 경우]

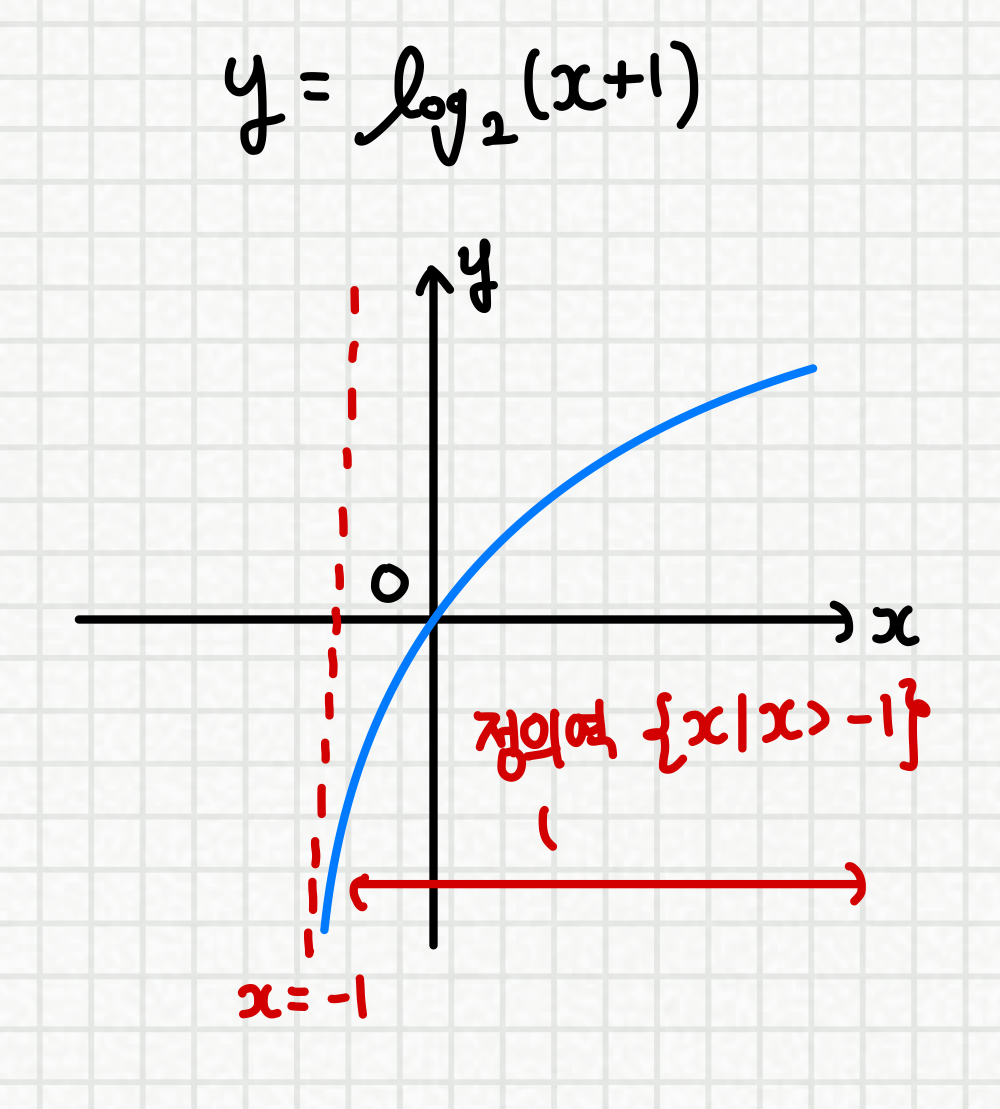
위 그림 처럼  x축 방향으로 평행이동만 했을 경우

(y축 방향으로의 대칭이동은 정의역 영향 X)

정의역의 부등호 방향은 그대로 이지만

점근선이 변했으므로

x > 0 -> x > -1 로 값이 변하게 됩니다

 

[대칭이동만 한 경우]

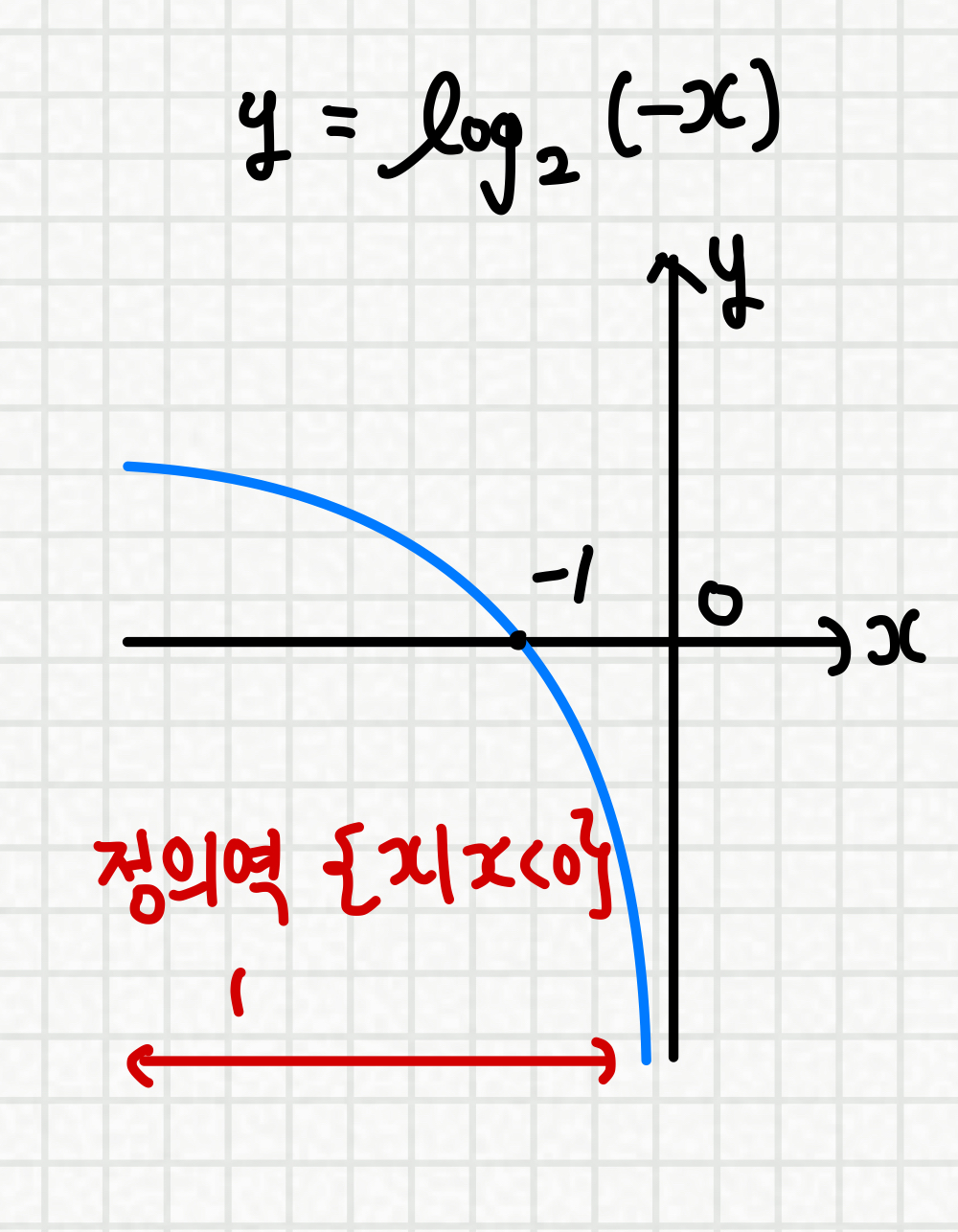
y축에 대하여 대칭이동만 했을 경우

(x축으로의 대칭이동은 정의역 영향 X)

정의역의 값은 그대로 이지만

x > 0 -> x < 0 으로 부등호 방향이 변하게 됩니다

[평행이동과 대칭이동 모두 한 경우]

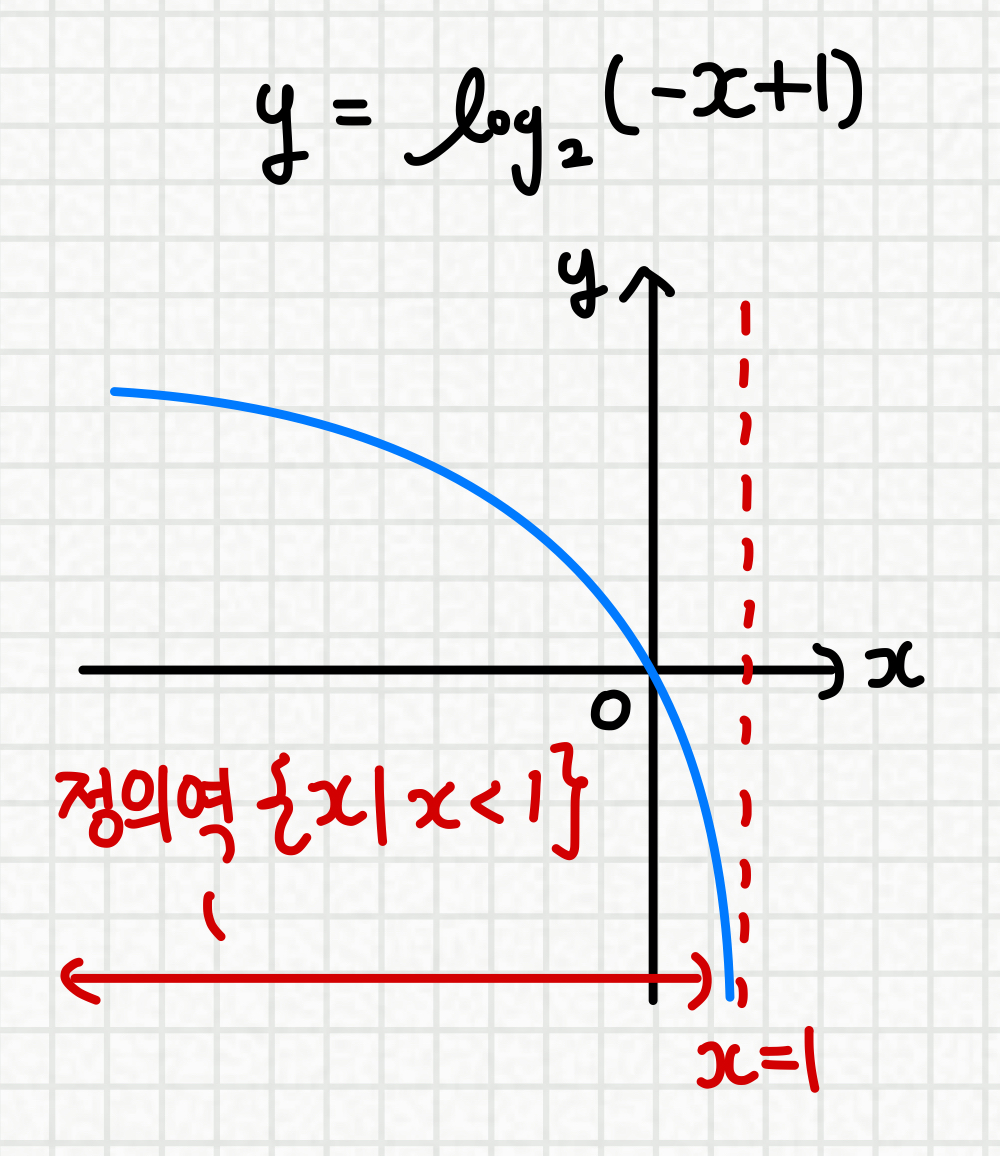
x축 방향으로의 평행이동과

y축에 대하여 대칭이동 했을 경우

 

정의역의 값과 부등호 방향 모두 변하게 됩니다

 

 

*중요

이때, 우리가 얻어가야 할 점은

나중에 배울 지수/로그 방부등식 - 치환 부분에서

 

로그를 치환할 때 

치환한 문자의 범위는 로그 함수의 치역과 같습니다

그러므로, 로그를 치환할 경우

항상 실수전체가 됩니다

 

(3) 로그함수의 정의역에 대한 고찰 (심화)

 

아래 두 함수를 비교해보도록 합시다

[로그함수의 정의역]

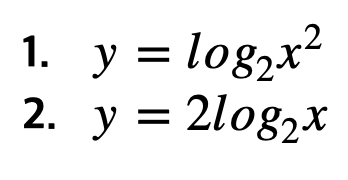
첫 번째 함수의 정의역은 얼마일까요?

정의역은 기본적으로 원래 형태에서 관찰해야 합니다

 

그러므로 아래와 같이 정의역을 구하는 것은 틀린 방법입니다

[정의역을 구하는 잘못된 방법]

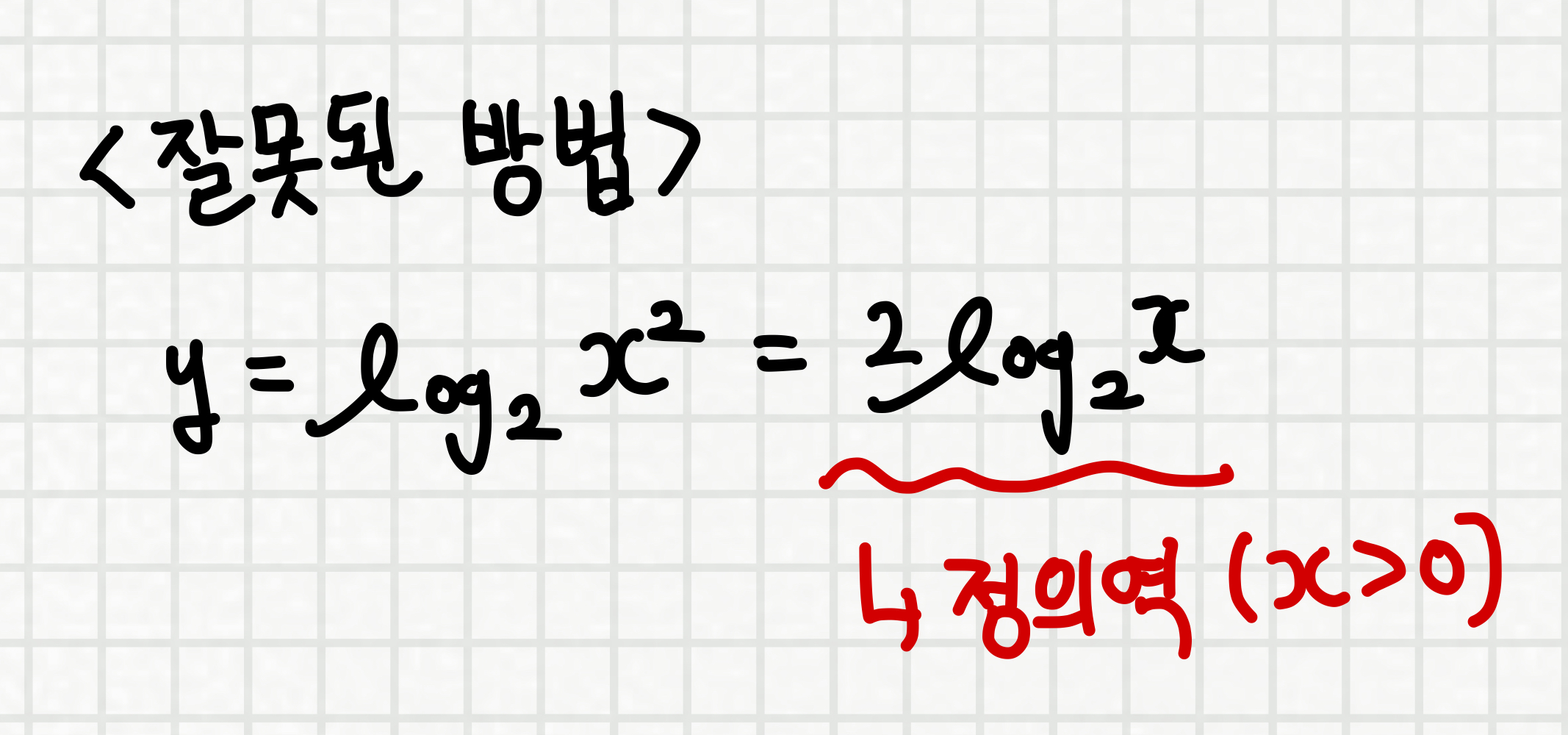
따라서, 로그의 정의 -> (진수) > 0 임을 이용하면

 

[정의역을 구하는 올바른 방법]

따라서

 

첫번째 로그 함수의 정의역 : 0이 아닌 실수 전체

두번째 로그 함수의 정의역 : 양의 실수

 

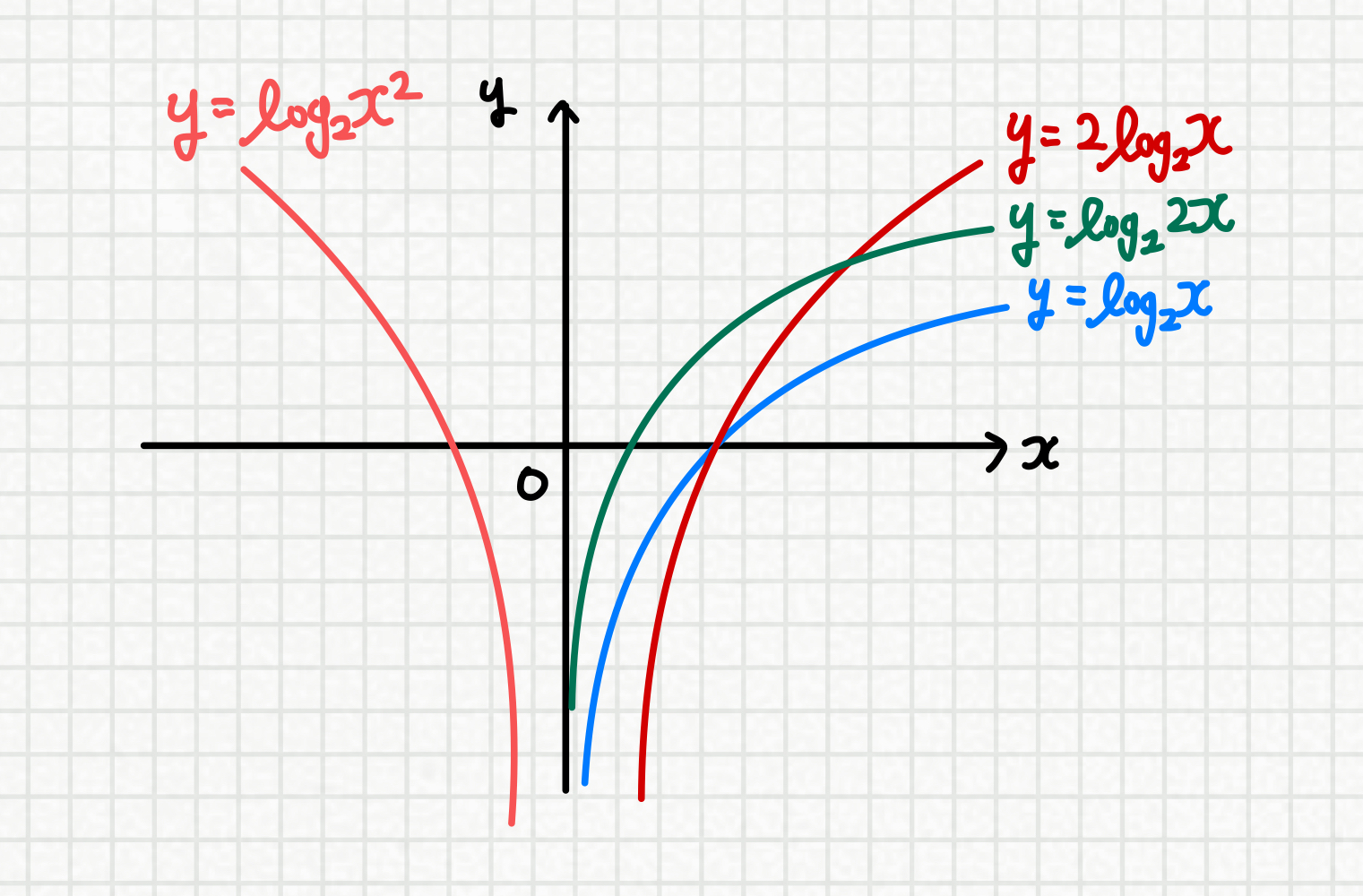
이므로, 두 그래프를 그려보면

[정의역 판단의 중요성]

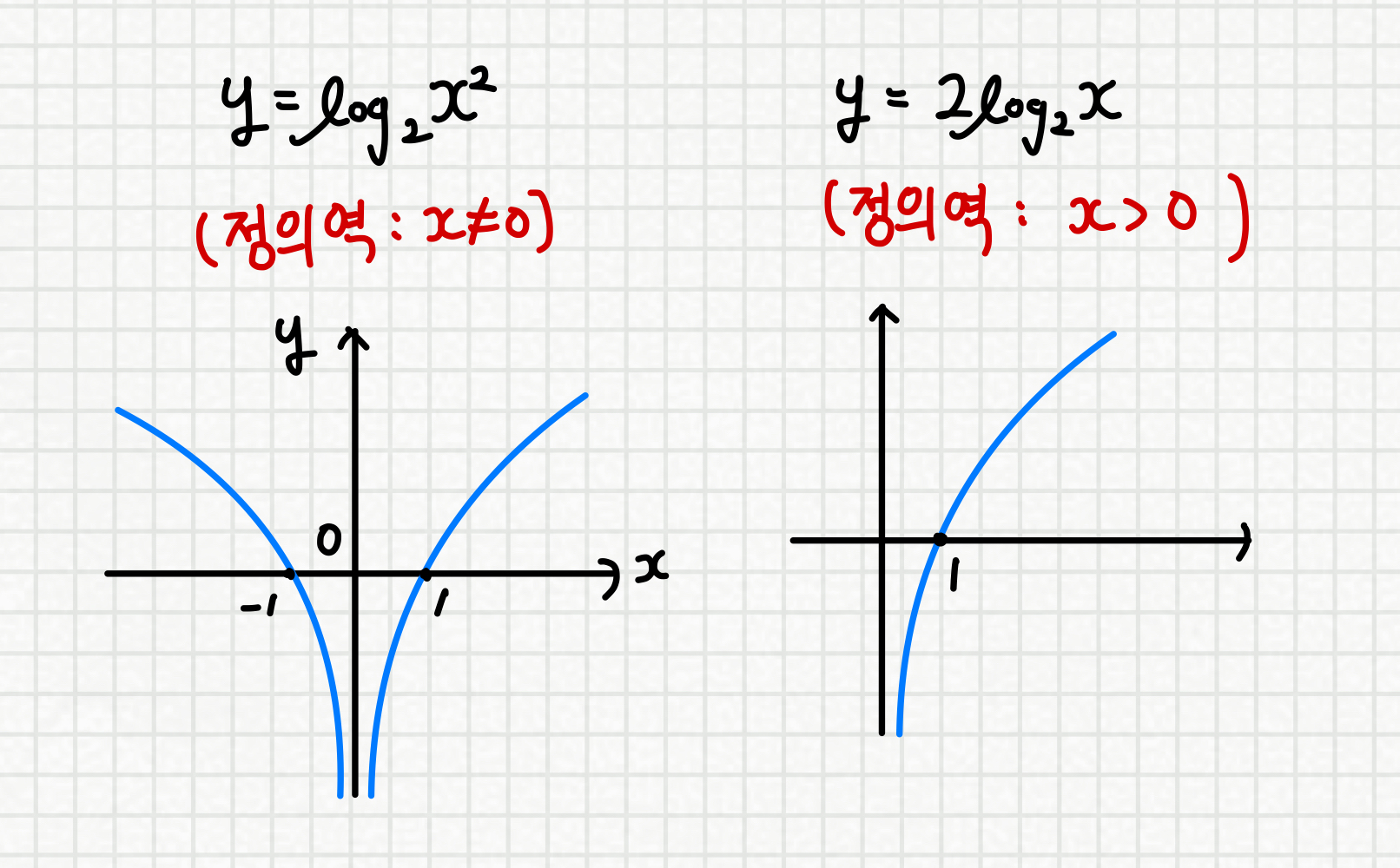
수식적으로는 차이가 없는듯 보이나

 

함수의 정의역 자체가 다르므로

서로 다른 함수가 됩니다.

 

 

 

 

3. 지수/로그 함수의 비율 관계!!

 

(1) 지수 함수의 비율 관계

[형태가 비슷해 보이는 두 지수함수]

위의 두 지수함수는 서로 어떤 관계가 있을까요?

대수적으로 좀 더 비교해 보면

 

[1:2 비율 관게]

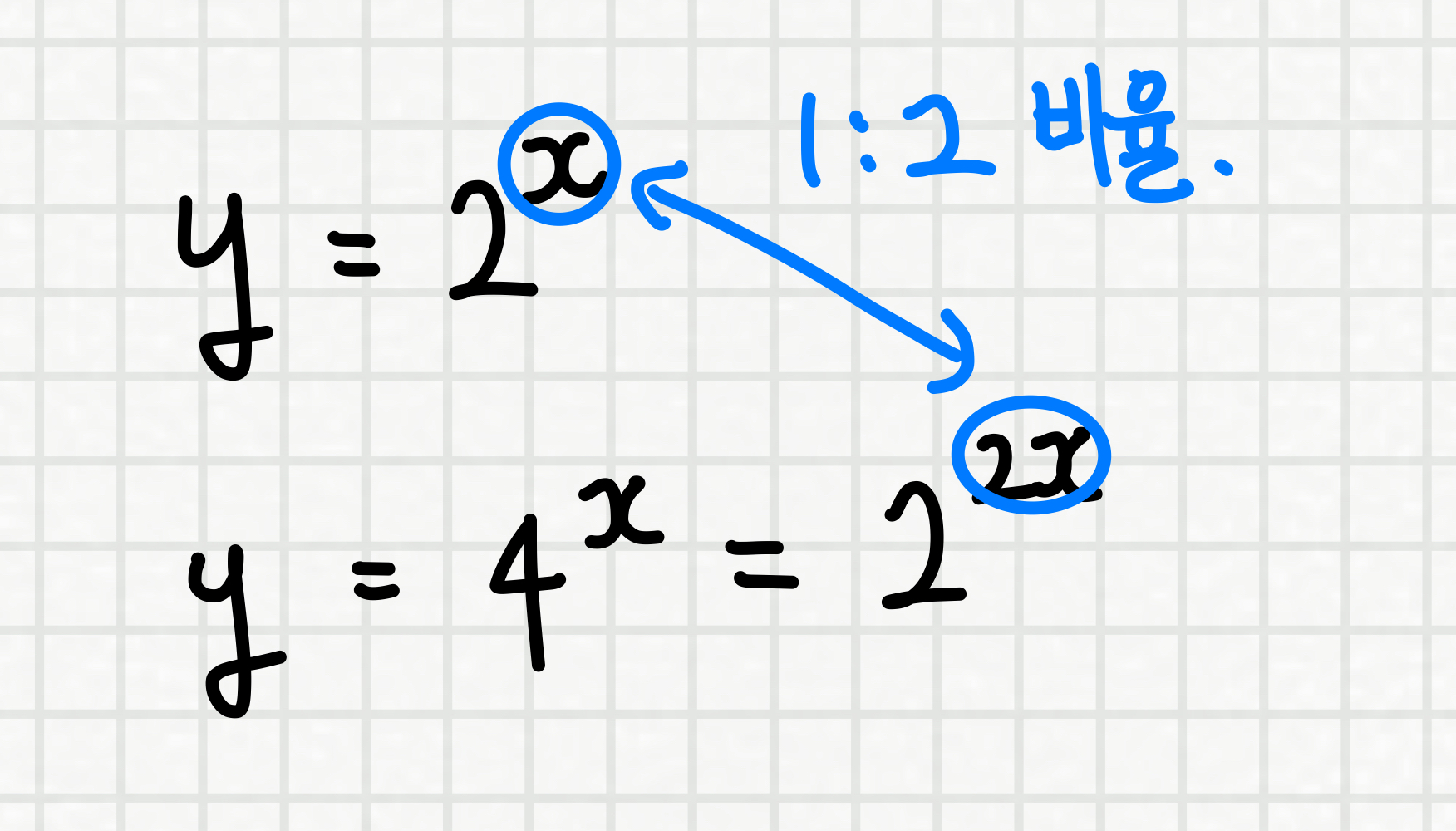
밑을 2로 동일하게 변형해주면

1:2의 비율관계를 발견할 수 있습니다

 

실제로, 그래프를 그려보면

 

[그래프 - 비율 관계]

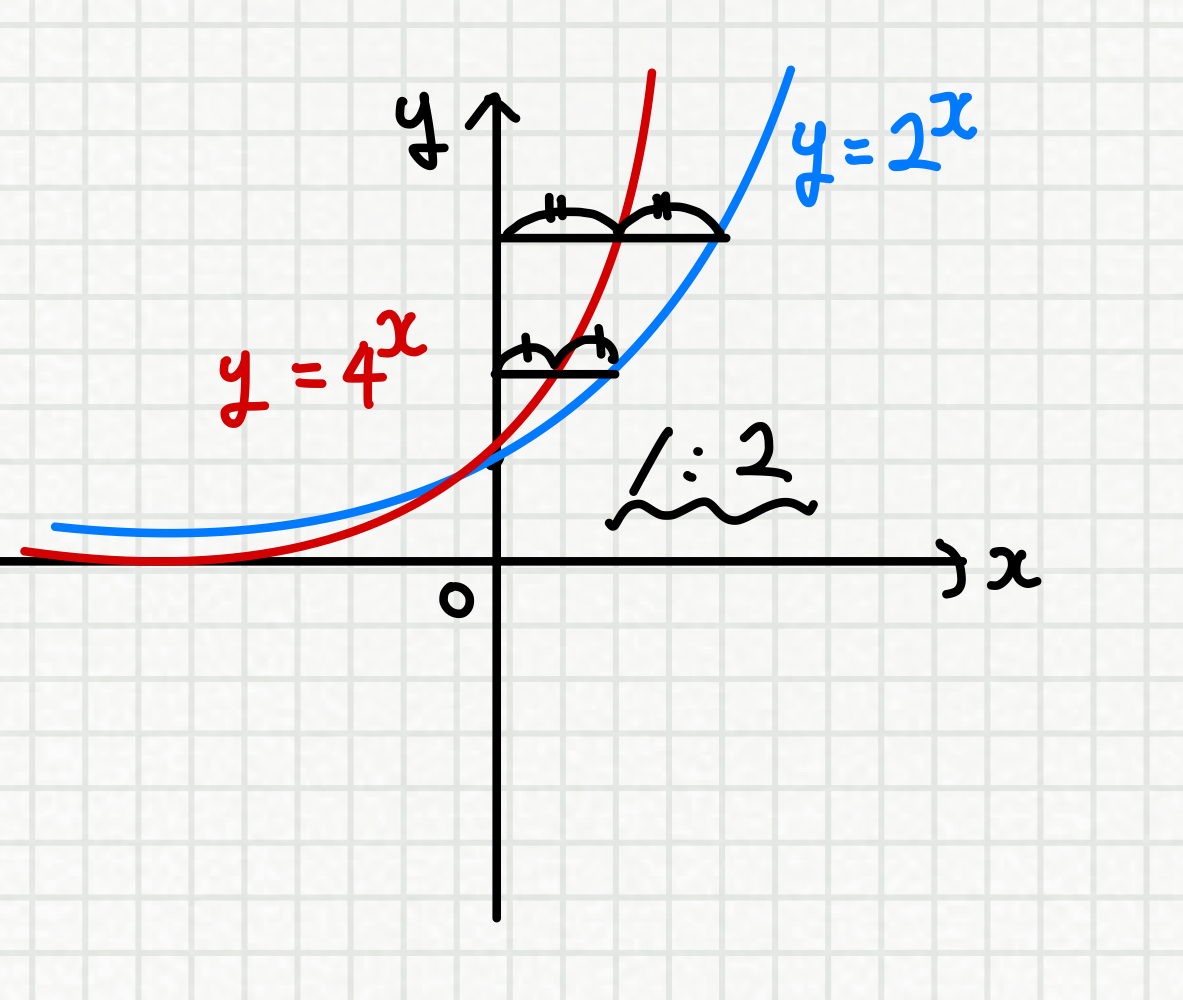
즉, y축과에 수선을 내렸을 때

 

길이의 비율이 1 : 2 임을 알 수 있습니다!

 

 

 

두 가지 예시를 더 살펴보도록 합시다

[지수함수의 비율 관계 - 추가 예시 (1)]

마찬가지로 먼저 대수적으로 비교해보면

 

[3:4 비율]

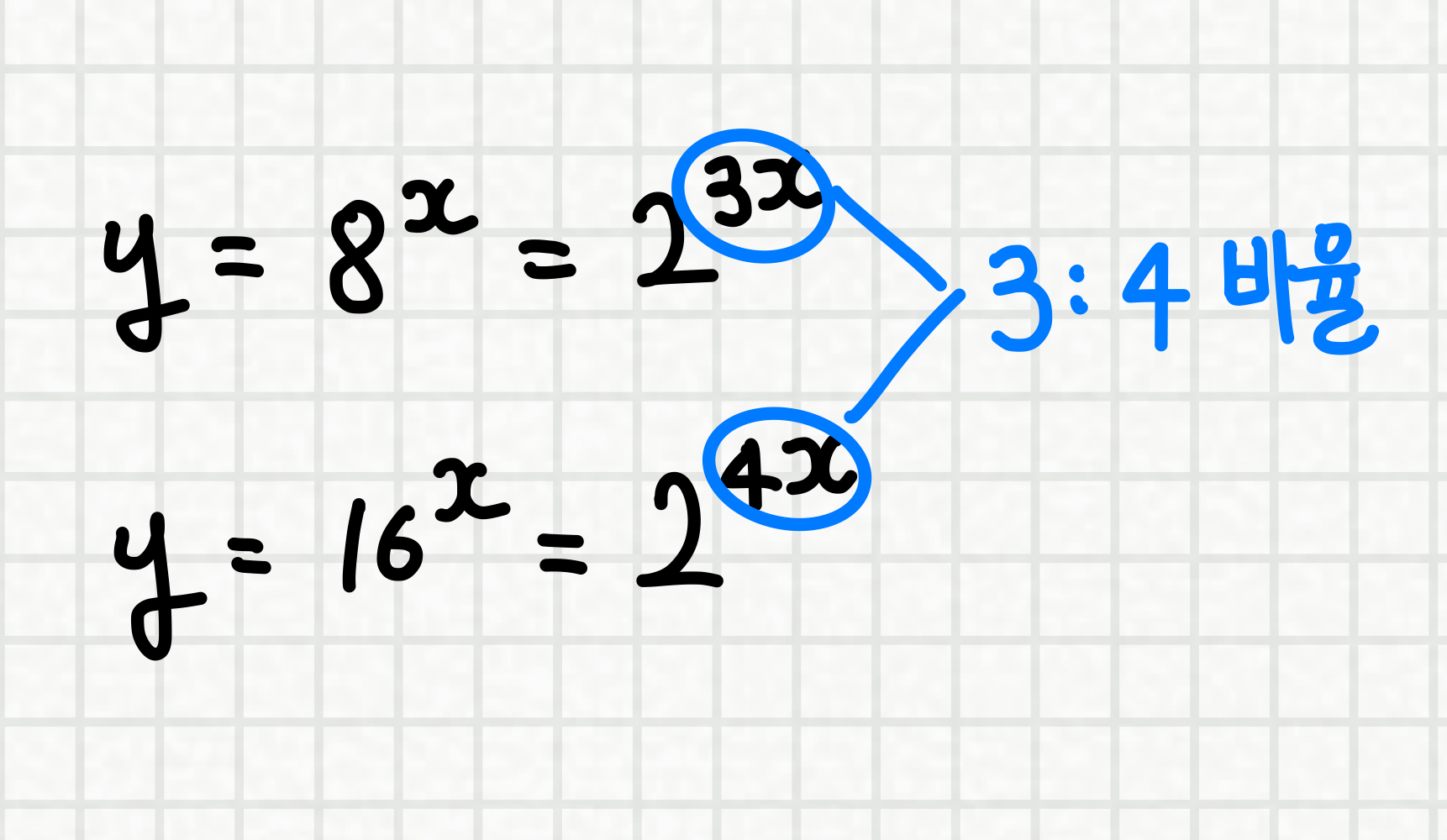
밑을 2로 동일하게 변형해 줬을 때

지수(x값)의 비율이 3:4임을 알 수 있습니다.

 

이후 그래프를 그려서 비율은 표시해보면

[지수함수 그래프 - 비율관계]

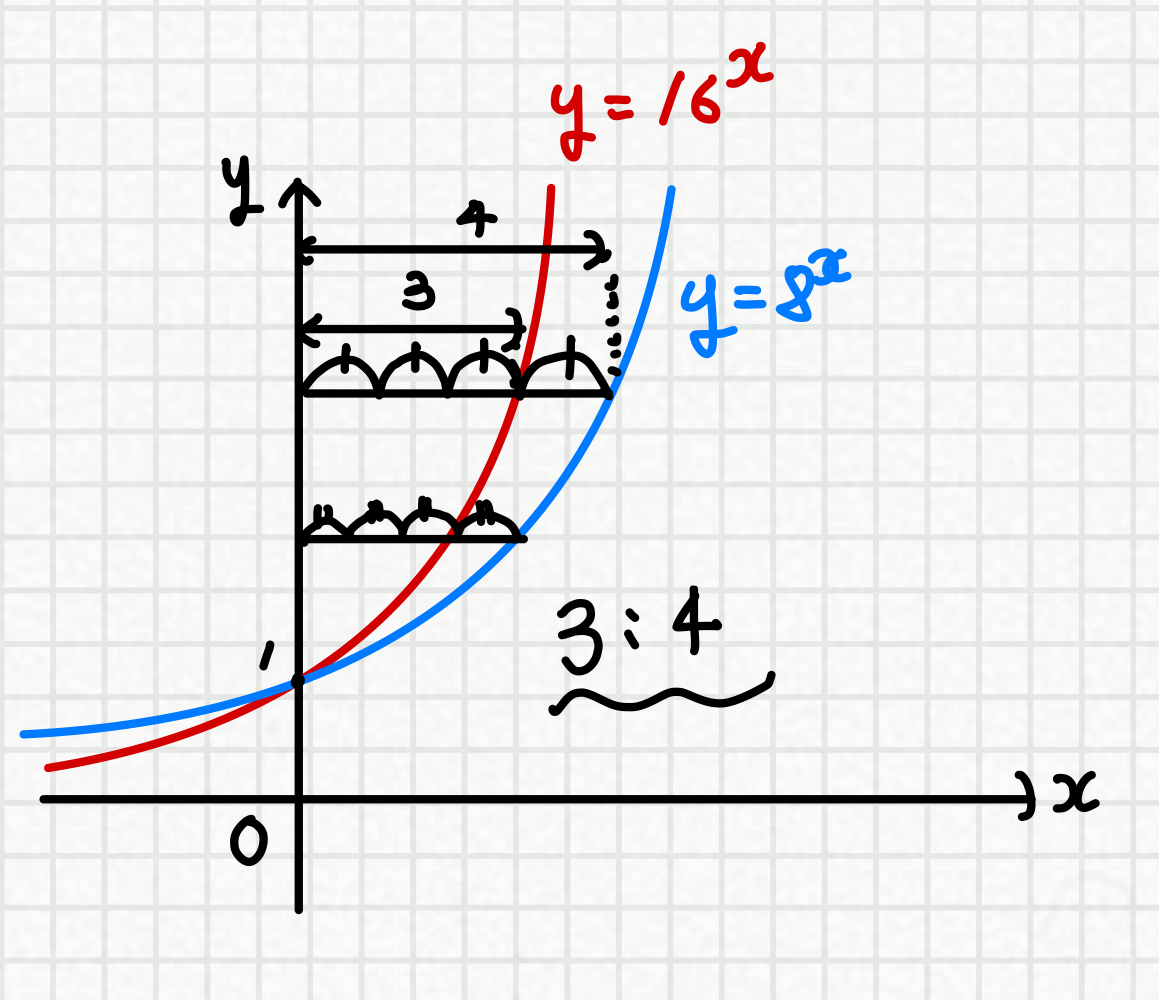
비율관계를 쉽게 알 수 있습니다!

 

 

 

 

마지막 지수함수 예시를 살펴보면

[지수함수의 비율관계 - 추가 예시 (2)]

[지수함수 그래프 - 비율관계]

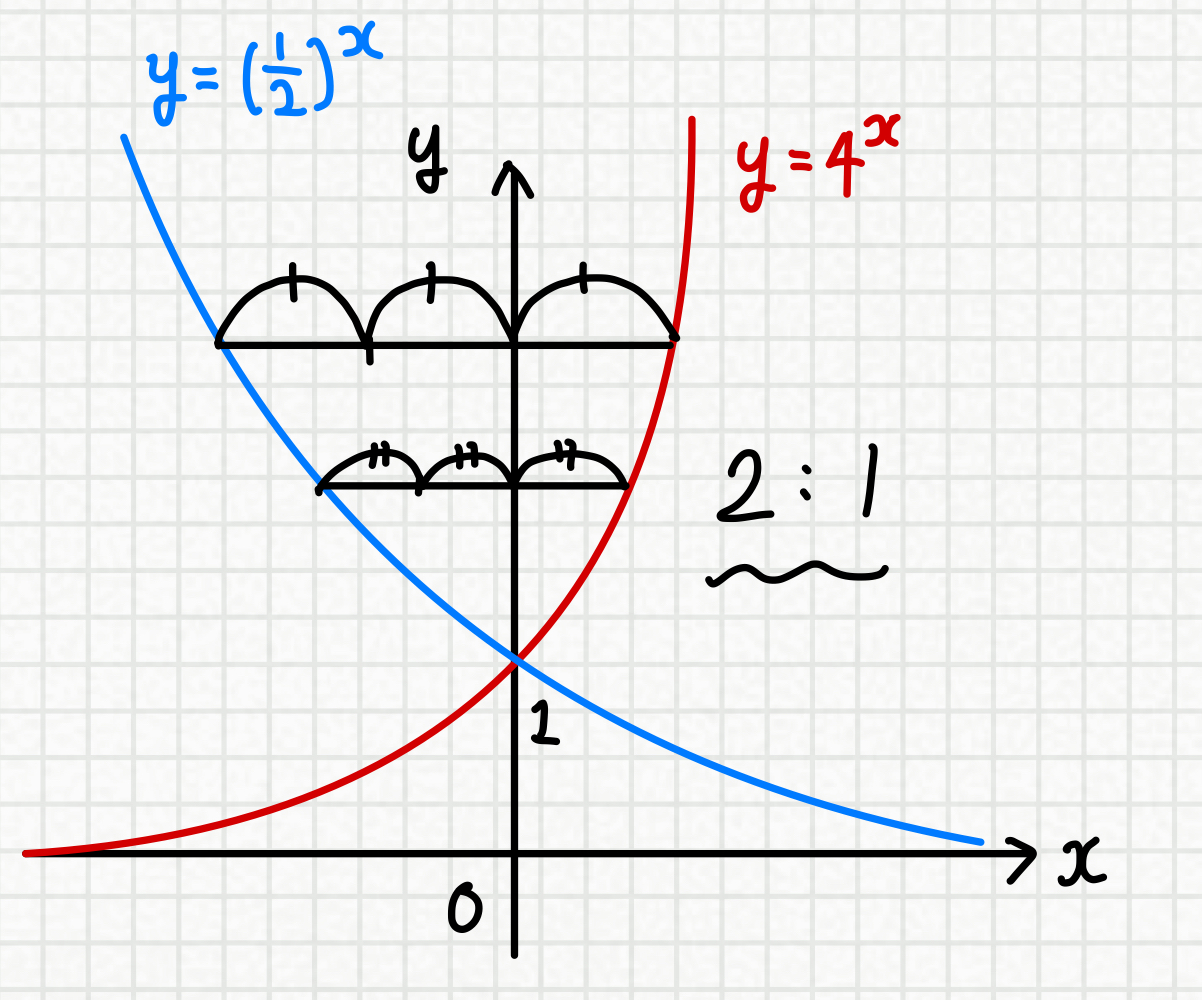
같은 방식으로 비율을 구할 수 있습니다~

 

 

 

 

(2) 로그 함수의 비율 관계

[헷갈리는 로그 함수]

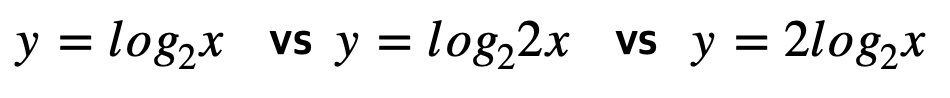
위 3가지 로그함수의 관계에 대해 알아보고

이번 포스팅을 끝마치도록 하겠습니다

 

 

먼저, 위의 두 로그함수는 어떤 관계일까요?

 

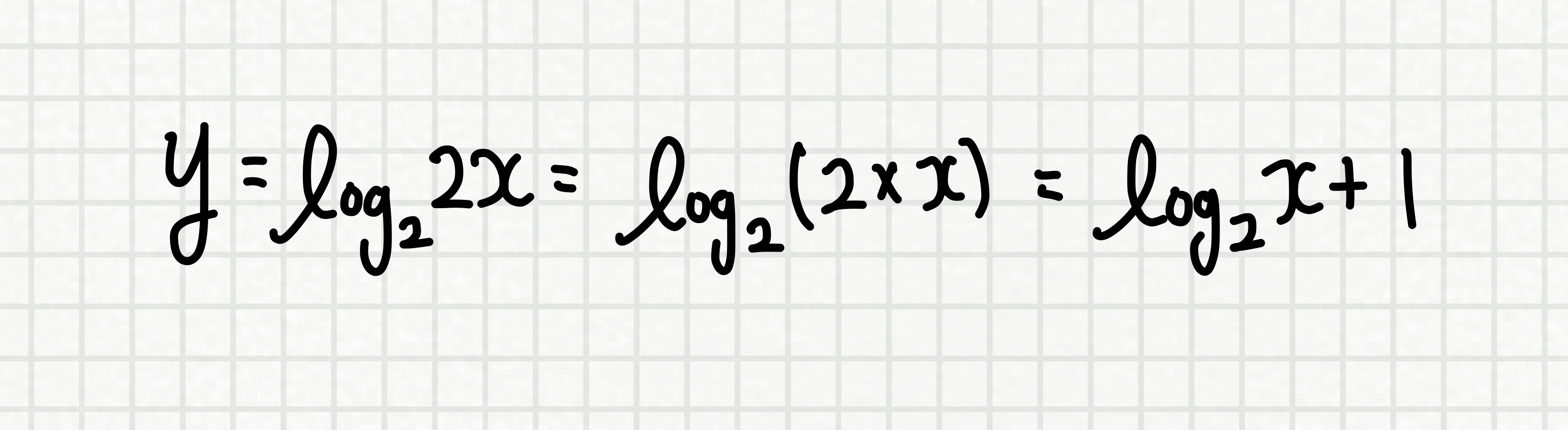
그렇죠

y축 방향으로 +1 만큼의 평행이동 관계임을 알 수 있습니다.

 

[평행이동 관계]

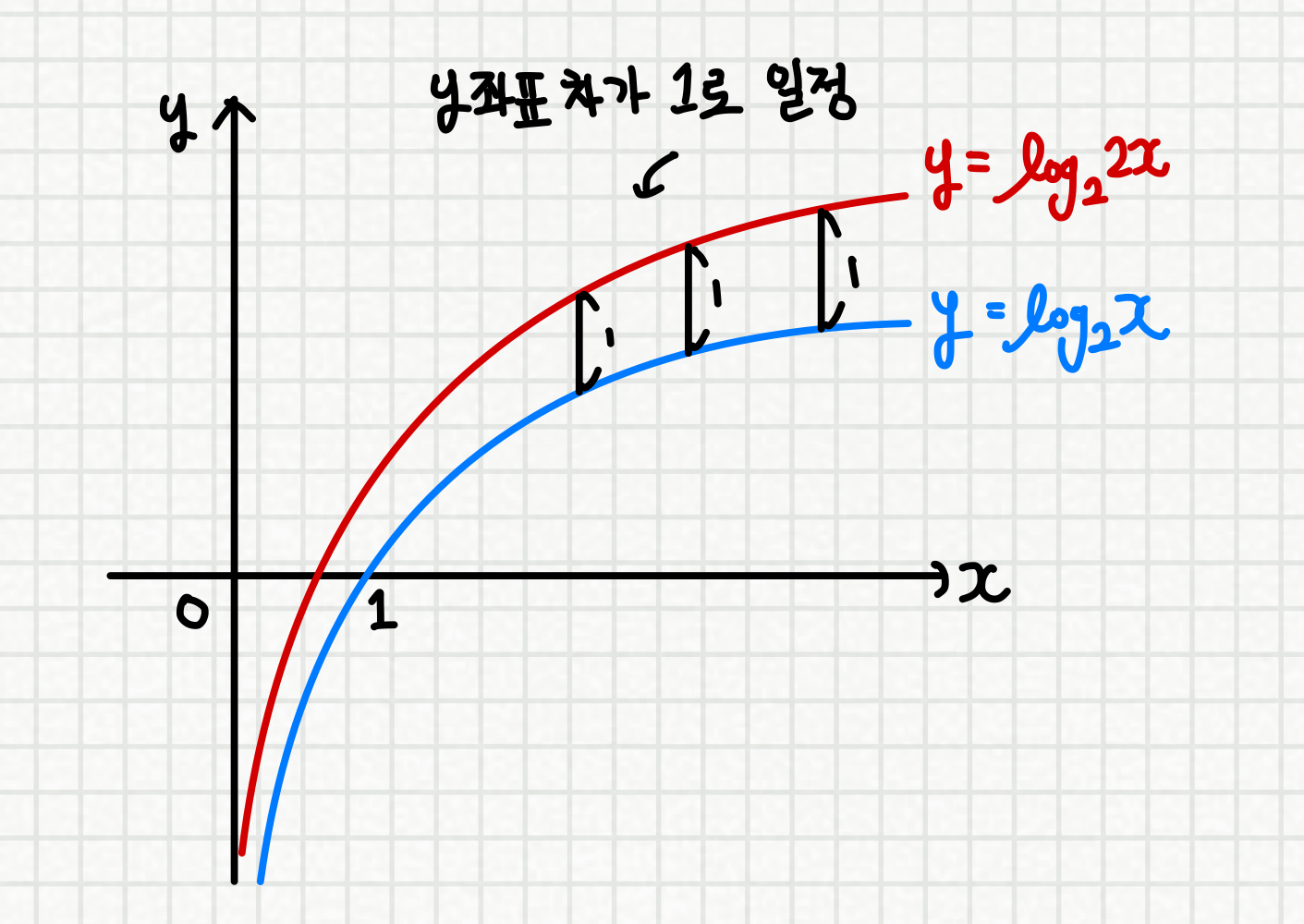
따라서,

y좌표의 차이가 1로 일정하게 되죠.

 

 

 

그렇다면, 다음 두 그래프는 서로 어떤 관계 일까요?

대수적으로만 보아도 y좌표의 비율이 1:2임을 알 수 있습니다

[로그 함수 - 비율관계]

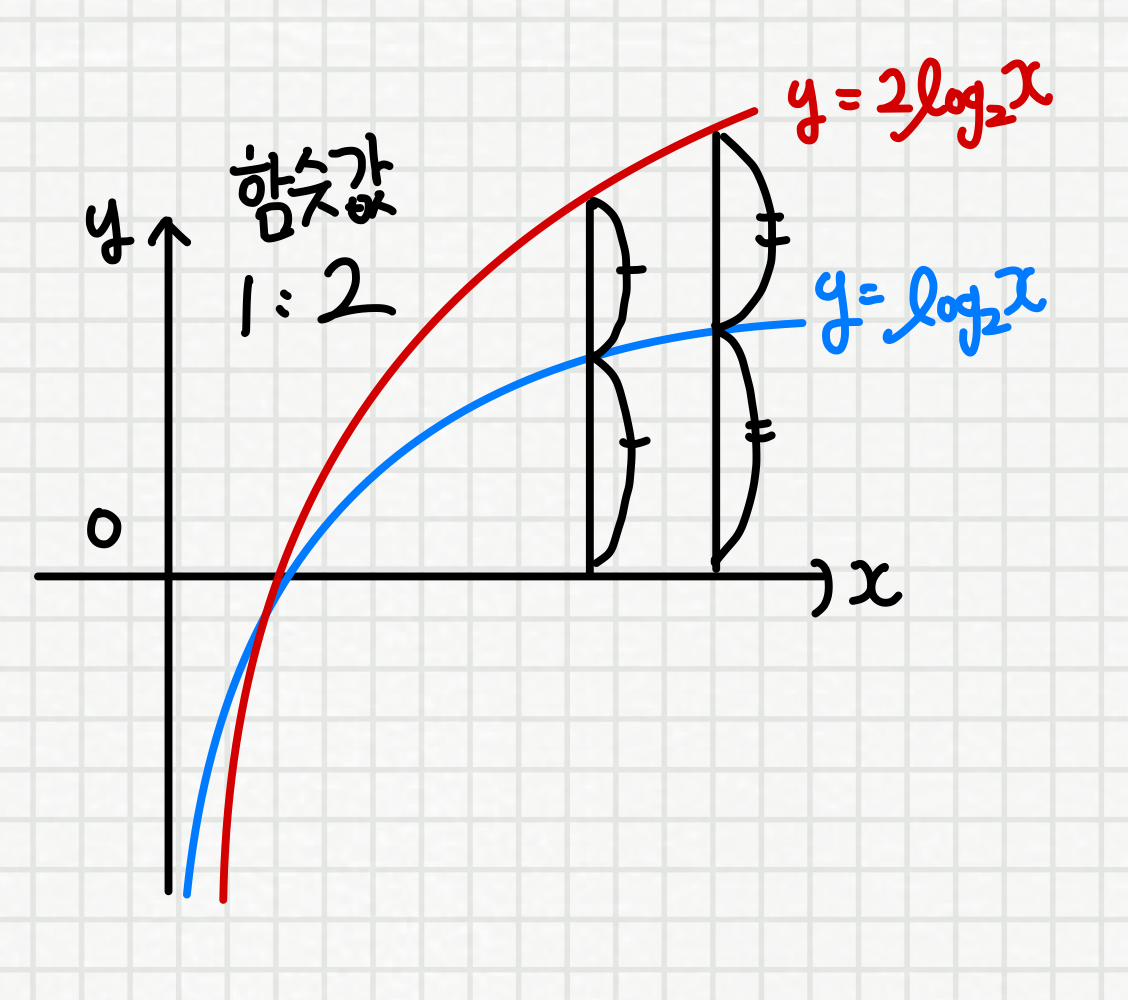
따라서, x값이 같을 때

y값의 비율이 1:2로 일정하게 됩니다 

 

정리해보면,

[로그 함수의 다양한 관계]

 

 

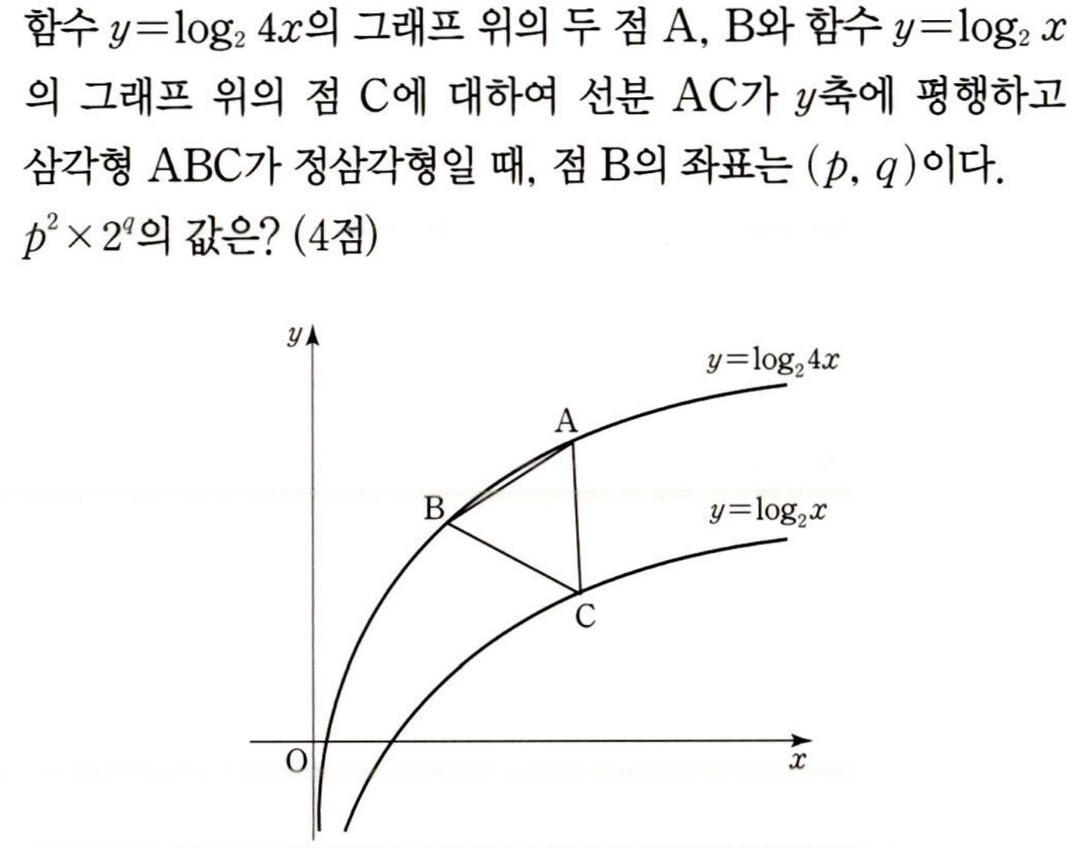
4. 문제 해설

 

[정의역의 중요성]

 

[해설]

 

마지막으로 아래 복습 문제 풀어보시고,

 

[비율 관계 - 복습문제]

 

다음 시간에는 < 지수/로그 함수 그래프 (3) - 역함수 >로 찾아뵙겠습니다~

 

화이팅!