[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
안녕하세요,
필수 유형에 대한
실전 개념 정리 입니다~
질문 사항은
아래 오픈챗 링크 혹은 메일로 보내주시면,
2시간 이내로 답변드리겠습니다.
오픈챗 링크 : https://open.kakao.com/o/srASNxef
메일 주소 : studying.all.night.1114@gmail.com
0. 대표문제
<1분 정도 고민해주세요!> - 그동안 배웠던 개념을 떠올리면 좋습니다~
비교적 쉬운 문제이지만,
우리가 얻어갈 수 있는 인사이트가 많은 문제입니다
1가지 방법으로만 풀지 말고 여러가지 방법으로 풀어보세요
관련 실전 개념을 먼저 설명드린 후, 해설은 마지막에 해드립니다!
1. 지수의 연쇄 법칙
(1) 활용 예시
지수 법칙 활용 문제를 풀 때는 지수의 형태를 관찰하다 보면,
쉽게 문제풀이에 대한 힌트를 얻을 수 있습니다.
바로 아래 문제 처럼 말이죠.
이런 유형을 처음 보신다면 당황하실 수도 있습니다.
그러나, 우리는 답의 형태와 문제 조건의 형태를 유기적으로 연결지어야 합니다.
따라서, 조건과 답의 형태를 관찰해보면
1. 4와 2의 연결성..!
2. (합)*(차) = (제곱의 차)..!
이 두가지 정보를 캐치해 낼 수 있습니다.
특히, 4와 2의 연결성이 매우 중요한데요.
이를 이용하면 아래와 같이 소위 "지수의 연쇄법칙"을 적용할 수 있습니다.
따라서, 위의 예시 문제에 대한 모법 답안은 다음과 같습니다.
(2) 지수의 연쇄 법칙 - 일반화
지수의 연쇄 법칙은 다음과 같이 일반화 할 수 있습니다.
마치 두개의 사슬 고리가 엮이듯,
두 개의 지수식이 지수법칙으로 연결 되는 현상을 지수의 연쇄 법칙이라 합니다
2. 지수의 연쇄 법칙 - 로그 관점의 해석
(1) 예시 - 로그 관점 해석
아까 지수의 연쇄법칙으로 해결한 위 문제를
이번에는 로그를 이용하여 해석해보겠습니다.
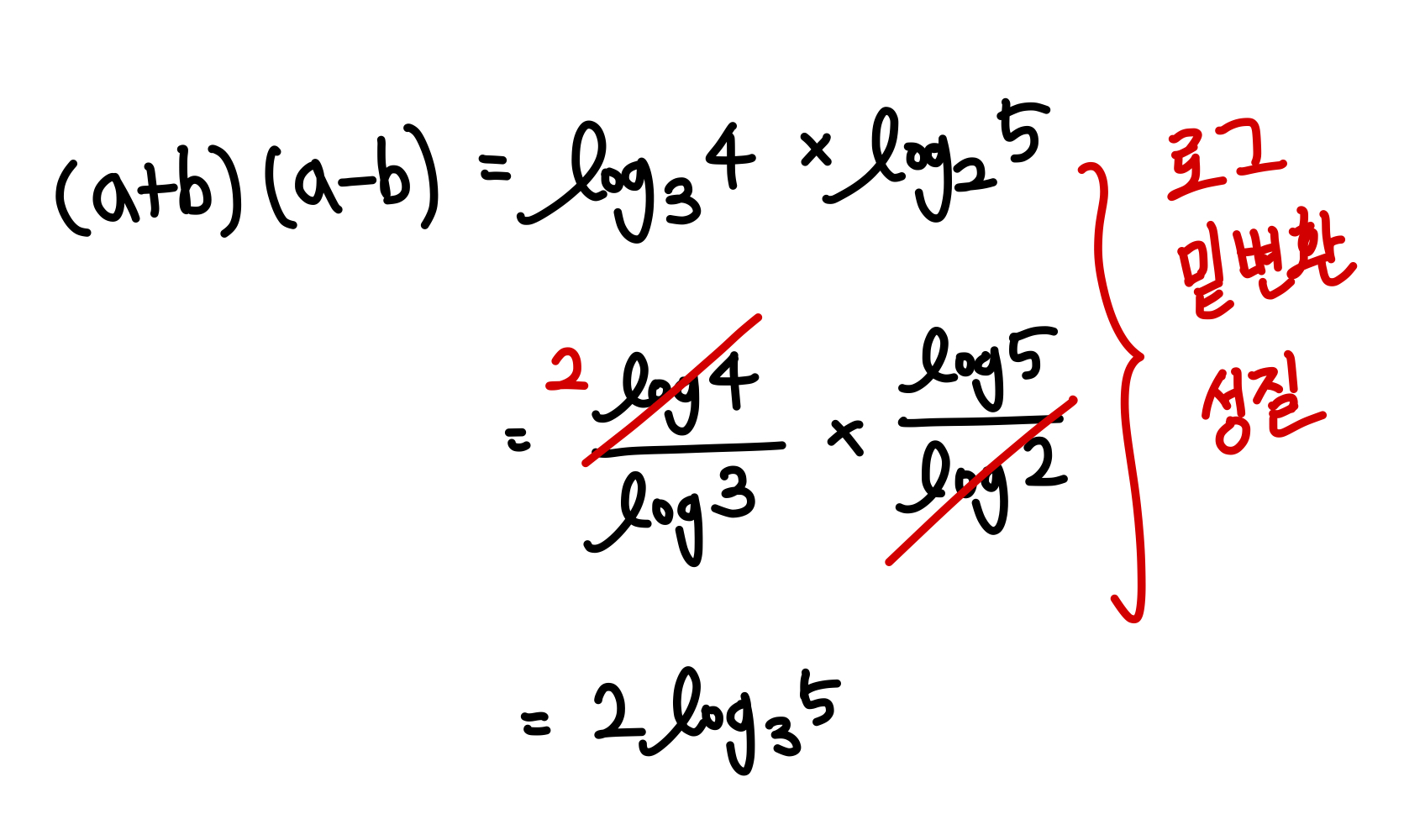
우리는 여기서 한가지 사실을 깨달을 수 있는데,
지수의 연쇄 법칙이란, 로그의 밑변환 성질을 이용한 로그의 곱과 유사한 성질을 가집니다!
로그의 밑변환 성질을 이용한 로그의 곱이 익숙하지 않으신 분들은
위의 빨간 글씨를 꼭 클릭해서 한 번 읽어보고 와주세요~
(2) 연쇄 법칙 일반화 - 로그 관점 해석
이러한 관점에서 지수의 연쇄법칙을 일반화 할 수 있습니다.
로그의 밑변환 성질을 활용할 수 있는 좋은 예시인 것 같습니다.
이제 마지막으로 처음에 봤던 문제들을 1. 지수의 연쇄 법칙 2. 로그의 밑변환 성질
두가지 방법으로 모두 풀어보도록 하겠습니다.
물론, 두 방법 모두 근본 원리는 같습니다
3. 문제 해설
(1) 문제의 조건과 답의 형태를 이용한 식변형
위 사진 처럼 답의 형태를 관찰해 보면
(x-3)과 (y-1)이 필요한 것을 알 수 있고
이러한 답의 형태에 맞추어 조건을 변형할 수 있습니다
이제 위의 형태를 보면 무엇인가 떠오르지 않나요?
맞습니다! 지수의 연쇄법칙을 바로 사용해주면 되겠네요
물론, 로그식으로 바꾼 뒤 로그의 밑변환 성질을 이용해 주어도 괜찮습니다
(2) 지수의 연쇄 법칙 or 로그의 밑변환 성질
오늘은 이처럼 지수의 연쇄법칙에 관해 배웠습니다.
아래 마무리 문제 스스로 풀어보시고! 질문이 있으시면 편하게 연락주세요~
다음에는 지수/로그 마지막 시간 - <상수 K의 도입> 으로 찾아뵙겠습니다
'밤샘수학 > 수학 1 [2단계-LIN]' 카테고리의 다른 글
| [수학 1 실전 개념] 6강 : 지수/로그 함수 그래프 (1) - 점근선&정점 (2) | 2023.03.28 |
|---|---|
| [수학 1 실전 개념] 5강 : 상수를 도입 하라 (0) | 2023.03.27 |
| [수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고 (0) | 2023.03.25 |
| [수학 1 실전 개념] 2강 : 거듭제곱근의 활용 - 특수 조건 (0) | 2023.03.23 |
| [수학 1 실전 개념] 1강 : 거듭제곱근의 정의 (0) | 2023.03.22 |