[수학 1 실전 개념] 2강 : 거듭제곱근의 활용 - 특수 조건

안녕하세요,
필수 유형에 대한
실전 개념 정리 입니다~
질문 사항은
아래 오픈챗 링크 혹은 메일로 보내주시면,
2시간 이내로 답변드리겠습니다.
오픈챗 링크 : https://open.kakao.com/o/srASNxef
메일 주소 : studying.all.night.1114@gmail.com
0. 대표 문제
<1분 정도 고민해주세요!> - 그간 배웠던 개념을 떠올리면 좋습니다

올해(2023년) 고2 내신 시험에 나올 가능성이 매우 높은 문제이니,
100% 이해를, 아니 150% 이해할 수 있도록 해야 합니다.
1. 자연수, 정수, 유리수 조건의 특수성
문제를 풀 때 자연수, 정수, 유리수 조건을 별 생각 없이 무시하는 경우가 종종 있습니다.
그러나, 수학 문제에서 "자연수, 정수, 유리수" 또한 문제를 푸는 핵심 조건이 됩니다.
아래 예시를 보면 자연수 조건이 꽤 흔하며, 문제의 중요한 풀이 KEY로 쓰임을 알 수 있습니다.

특히, 거듭제곱근 문제에서는 자연수 조건이 더욱 자주 나오므로
자연수 조건이 나왔을 때의 행동강령을 알고 체화시켜야 합니다.
2. 자연수, 정수, 유리수 조건을 이용한 문제풀이
관련 문제를 풀기 위해서는 다음을 행동강령으로 받아들이고 문제에 적용시킬 줄 알아야 합니다.

당연히, 정수와 유리수 또한 미지수를 도입하여 식에 대입하여야 합니다.
마찬가지로 아래와 같은 사실이 알려져 있습니다.
이는 우리가 무의식 중에 쓰는 명제이지만 짚고 넘어갈 필요가 있습니다.

위 두 문장을 받아들였다는 전제 하에 한 가지 예시를 들어 보겠습니다.
다음식이 성립하기 위한 x의 조건은 무엇일까요?

혹시 x는 4의 약수라고 생각하셨나요?
...
틀렸습니다..! 정답은 4의 약수가 아닌 "12의 약수"가 되어야 합니다.
그 이유는 8을 그대로 두고 생각하면 안되고, "소인수 분해 된 상태"로 바꿔주어야 합니다.
즉, 아래 상태에서 약수/배수 등을 생각해야 합니다

따라서 x는 12의 약수 => 1, 2, 3, 4, 6, 12 가 됩니다.
비슷한 원리를 이용한 예시 1가지를 더 보면,

위의 예시도 마찬가지로 12의 배수로 해석하면 안되고!
먼저 "소인수 분해 된 상태"로 바꿔주어야 합니다.

따라서, x는 12의 배수가 아니라 "2의 배수"가 되어야 합니다.
그럼 이제 다시 원래 문제를 살펴볼까요
3. 문제 해설

먼저, 정수에 밑줄긋고 새로운 미지수 X를 도입해 보도록 하겠습니다.

따라서 아래와 같은 방정식을 세울 수 있습니다
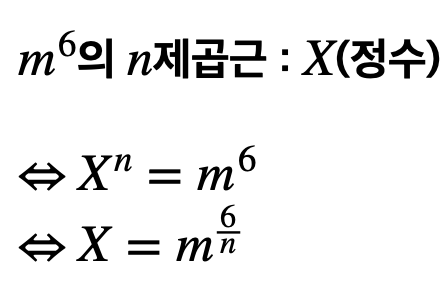
이때 X와 m이 자연수 이므로 (6/n)이 자연수가 되어야 합니다.
(그러나, 정확한 n의 개수를 구하기 위해서는 m을 소인수 분해된 형태로 바꾸어야 합니다)
(1) m = 7 일 때,
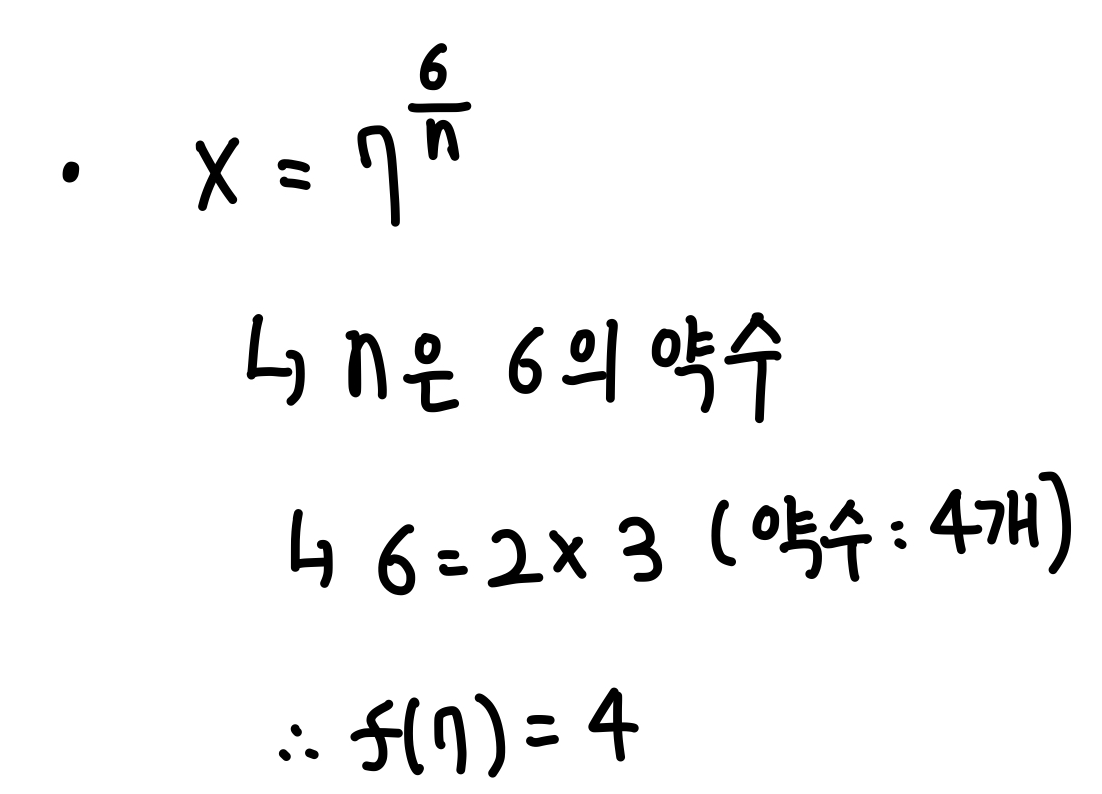
(2) m = 9 일 때,
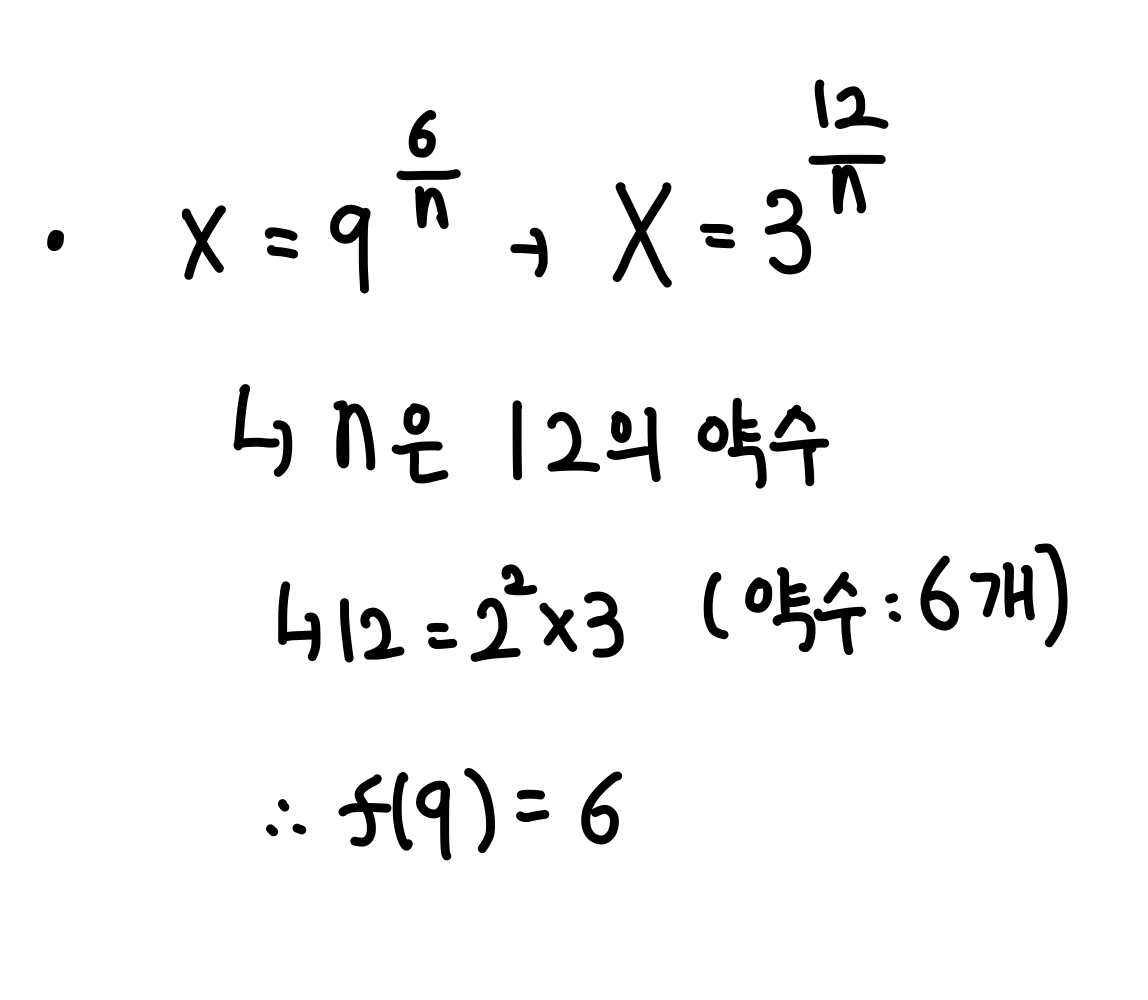
(3) m = 16 일 때,
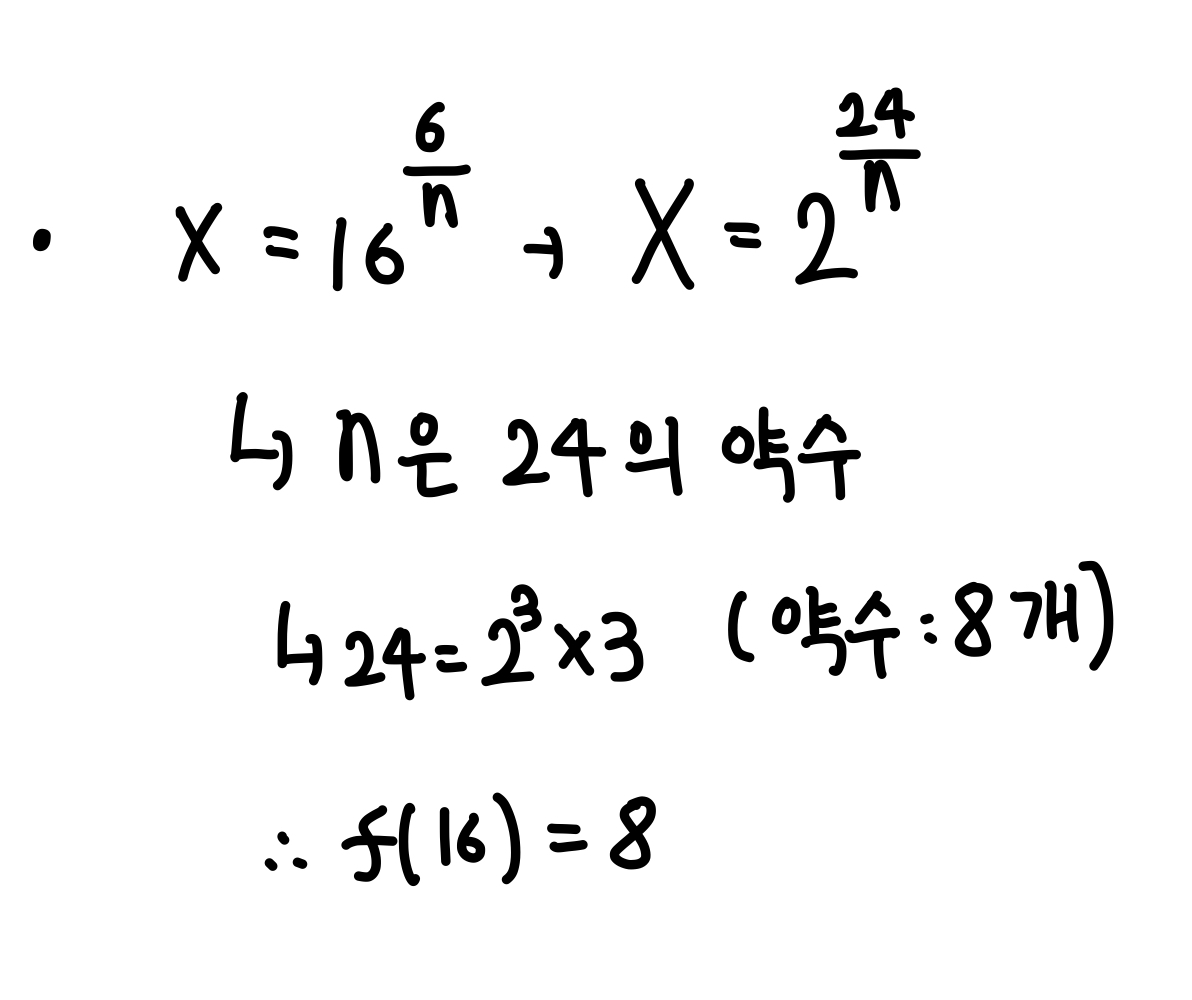
by (1), (2), (3) => 답) (4-1) + (6-1) + (8-1) = 15 (*주의 : n은 1이 아니라고 했으므로 1개씩 빼줘야 함)
'밤샘수학 > 수학1 실전 개념' 카테고리의 다른 글
| [수학 1 실전 개념] 6강 : 지수/로그 함수 그래프 (1) - 점근선&정점 (2) | 2023.03.28 |
|---|---|
| [수학 1 실전 개념] 5강 : 상수를 도입 하라 (0) | 2023.03.27 |
| [수학 1 실전 개념] 4강 : 지수의 연쇄법칙 (0) | 2023.03.26 |
| [수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고 (0) | 2023.03.25 |
| [수학 1 실전 개념] 1강 : 거듭제곱근의 정의 (0) | 2023.03.22 |
댓글
이 글 공유하기
다른 글
-
[수학 1 실전 개념] 5강 : 상수를 도입 하라
[수학 1 실전 개념] 5강 : 상수를 도입 하라
2023.03.27 -
[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
2023.03.26 -
[수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고
[수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고
2023.03.25 -
[수학 1 실전 개념] 1강 : 거듭제곱근의 정의
[수학 1 실전 개념] 1강 : 거듭제곱근의 정의
2023.03.22
댓글을 사용할 수 없습니다.