[수학 1 실전 개념] 1강 : 거듭제곱근의 정의

안녕하세요,
필수 유형에 대한
실전 개념 정리 입니다~
질문 사항은
아래 오픈챗 링크 혹은 메일로 보내주시면,
2시간 이내로 답변드리겠습니다.
오픈챗 링크 : https://open.kakao.com/o/sdqZK0bf
메일 주소 : studying.all.night.1114@gmail.com
0. 대표 문제
<1분 정도 고민해주세요!> - 그간 배웠던 개념을 떠올리면 좋습니다

ㄱ 에서 처음에 함정에 걸렸을 수도 있고,
ㄷ 은 표현이 어색한 것 같기도 하고
ㄹ 은 맞는 것 같고
ㅁ 은 당연하게 느껴질 것입니다
다만, 수학은 항상 의심하고 또 의심해야 합니다.
위 문제에 유의하며 개념 정리하러 가봅시다! (답은, 마지막에 해설해 드립니다.)
1. 거듭제곱근 이란?
"거듭제곱근"은 "거듭제곱" + "근" 의 합성어 입니다.
즉, "여러번 곱한 것"과 관련된 "방정식의 근"의 의미를 내포하고 있죠.
이를 좀 풀어서 설명하면 다음과 같습니다.

(단, a는 실수이고 n은 2이상의 자연수)
즉, "8의 세제곱근"이라고 하면

위 내용이 8의 세제곱근의 의미가 됩니다.
8의 세제곱근의 값은 얼마인가요?
위에서 생각해둔 의미에 의해서
아래 방정식을 풀어주면 됩니다.

이때 실수 범위에서 1개,
복소수 범위에서 2개의 근이 나오므로
총 3개의 근이 존재함을 알 수 있습니다.
a의 n제곱근은 무조건 n개라고 볼 수 있는데
이는 아래와 같은 사실이 알려져 있기 때문입니다.

a의 n제곱근을 "복소수 범위"에서 볼 때 성립하는 것이고,
일반적으로 고등학교 수1에서는 a의 n제곱근을
"실수 범위"에서만 살펴 봅니다. 실수 범위에서는
a의 n제곱근에 대해 그래프를 그려 해석할 수 있습니다.
2. 거듭제곱근 중 실수인 것
a의 n제곱근 중 실수인 것을 구하기 위해
다음 내용을 알고 있어야 합니다.

즉, a의 n제곱근 중 실수를 구할 때는
식을 보고 계산하는 것이 아니라
다음과 같이 기하적(그래프) 관점에서 해석해야 합니다.

이 때 n이 짝수인지 홀수인지에 따라
=> y축 대칭(우함수)과 원점 대칭(기함수)이 정해지고
a의 부호(+, 0, -)에 따라
=> 교점의 개수 및 위치가 달라지게 됩니다.
따라서 다음 표 처럼 총 6가지 종류가 나오게 됩니다.
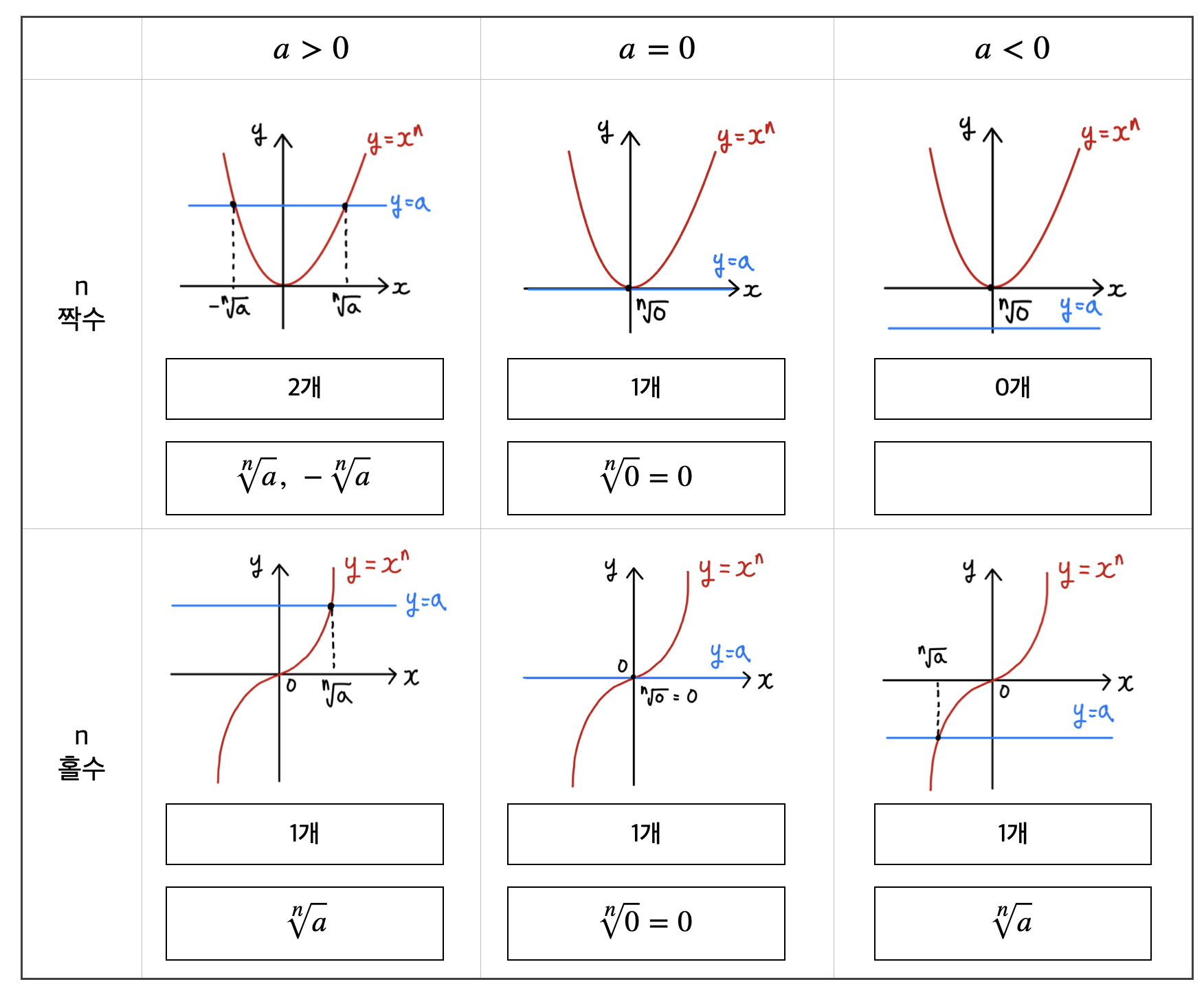
우리가 주의 해야할 건
n이 짝수일 때 a가 음수일 수 없다는 사실 입니다.
즉, 아래와 같이 쓰는 것은
실수범위에서 표기 자체가 불가능 합니다.
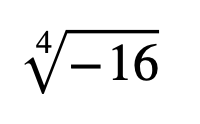
이를 정리하면

3. 문제 해설

ㄱ. -8의 제곱근은 2개이다. (O)
=> 실수라는 말이 없으므로,
복소수 범위까지 생각해 주면
2개가 됩니다.
ㄴ. 5의 세제곱근 중 실수는 1개이다. (O)
=> 범위가 실수이므로,
그래프를 그려보면
n이 홀수, a가 양수에서 한 점에서 만난다.
ㄷ. 네제곱근 16중 실수는 +2, -2 이다. (X)
=> 16의 네제곱근과 달리
네제곱근 16은 계산식입니다.
(즉, 네제곱근 16 = 2)
ㄹ. a의 n제곱근 중 실수의 개수가 1개라면, n은 홀수이다. (X)
=> n이 짝수이며, a가 0일 때 또한, 1개 존재합니다.
ㅁ. (X)
=> 아래와 같은 반례가 존재합니다.
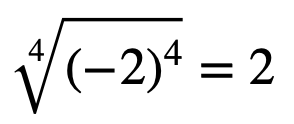
따라서, ㄱ, ㄴ 총 2개가 답이 됩니다.
'밤샘수학 > 수학1 실전 개념' 카테고리의 다른 글
| [수학 1 실전 개념] 6강 : 지수/로그 함수 그래프 (1) - 점근선&정점 (2) | 2023.03.28 |
|---|---|
| [수학 1 실전 개념] 5강 : 상수를 도입 하라 (0) | 2023.03.27 |
| [수학 1 실전 개념] 4강 : 지수의 연쇄법칙 (0) | 2023.03.26 |
| [수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고 (0) | 2023.03.25 |
| [수학 1 실전 개념] 2강 : 거듭제곱근의 활용 - 특수 조건 (0) | 2023.03.23 |
댓글
이 글 공유하기
다른 글
-
[수학 1 실전 개념] 5강 : 상수를 도입 하라
[수학 1 실전 개념] 5강 : 상수를 도입 하라
2023.03.27 -
[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
[수학 1 실전 개념] 4강 : 지수의 연쇄법칙
2023.03.26 -
[수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고
[수학 1 실전 개념] 3강 : 지수법칙 활용 - 유연한 사고
2023.03.25 -
[수학 1 실전 개념] 2강 : 거듭제곱근의 활용 - 특수 조건
[수학 1 실전 개념] 2강 : 거듭제곱근의 활용 - 특수 조건
2023.03.23
댓글을 사용할 수 없습니다.