[수학 1 실전 개념] 14강 : 삼각함수의 정의

안녕하세요, 밤샘공부 입니다~
질문 사항은
아래 오픈챗 링크 혹은 메일로 보내주시면,
2시간 이내로 답변드리겠습니다.
오픈챗 링크 : https://open.kakao.com/o/srASNxef
메일 주소 : studying.all.night.1114@gmail.com
오랜만에 글을 쓰네요. 오늘도 여러분께 수학적 통찰을 주는 강의가 되었으면 합니다.
이번엔 좌측정렬로 강의를 써 보았는데, 무엇이 더 편한지 피드백 해주시면 감사하겠습니다 :)
1. 대표 문제
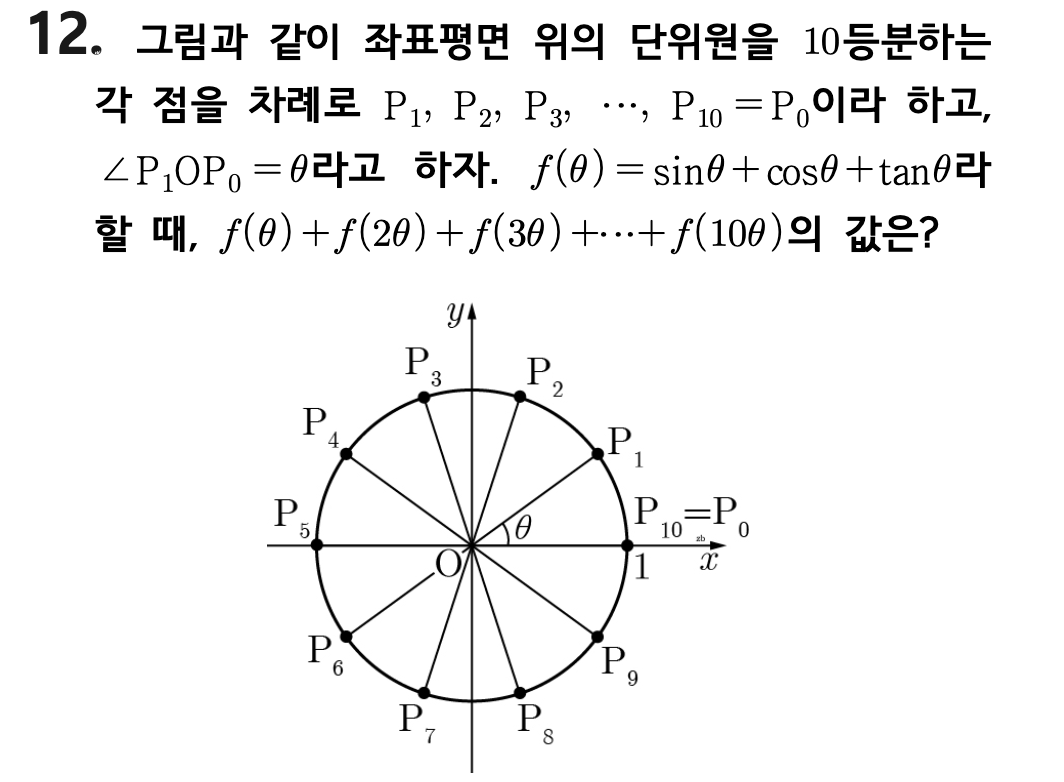
당연히, 위 문제를 하나하나 대입해가며 풀지는 않을 겁니다. 모종의 '대칭성' 혹은 '주기성'을 활용해야 할듯 싶은데, <삼각함수의 정의에 대한 개념>이 완벽히 이해되고 머릿속에 정립되지 않았다면 풀이가 꽤 혼란스러울 듯 하네요. 언제나 그렇듯 수학은 "스킬을 익히는 것" 보다 "스킬을 창조하는 것"이 중요한 학문입니다. "스킬을 단순히 외우는 것"은 물고기를 잡는 법을 배우지 않고 물고기를 구걸하여 얻은 것과 같습니다. 여러분이 물고기를 직접 잡는 방법을 배우지 못한다면 계속 배고픔에 굶주릴 수 밖에 없으며 영원히 구걸만을 하며 살아야 합니다. 수학도 마찬가지 입니다. 직접 스킬을 만드는 방법을 모른다면 여러분은 영원히 학원/인강에 기대어 구걸할 수 밖에 없습니다. 여러분이 진정으로 수학을 잘하고 싶으시다면 '개념을 기반으로 스킬을 스스로 만들 수 있는 능력'을 길러야 합니다.
해설은 강의 마지막에 나와있으며, 일단은 <삼각함수의 정의>에 대하여 같이 살펴보도록 합시다.
2. 삼각함수의 정의
(1) 호도법의 등장 + 동경의 정의
① 호도법이란.
우리는 여지껏, 각도 단위만 써왔습니다. 90도 150도 180도 처럼 말이죠. 이는 분명히 직관적인 방법이며 우리는 이미 해당 단위에 익숙해져 있습니다. 그러나 수학/과학 계에서는 '도' 단위가 생각보다 불편했습니다. 우리가 수학에서 쓰는 수들은 기본적으로 단위가 없습니다. 무차원이라고도 하죠. 그렇기에 90 '도'가 수식에서 꽤나 불편하게 작용했습니다. 예를 들어 단위를 깜빡하고 90이라고만 쓴다면. 이 숫자가 뜻하는 것이 90도인지, 실수 90인지 헷갈리는 위험성이 존재했습니다.
그렇기에 수학자들은 각도의 단위를 없애기 위해 호도법을 창안하게 됩니다. 마치 우리가 "세슘원자가 9192631770번 진동할 때를 1초로 정의"하는 것 처럼 말이죠. 즉, "반지름과 호의길이가 같은 부채꼴의 중심각을 1라디안이라고 정의" 하게됩니다. '라디안도 단위인거 아니야?'라고 생각하실 수 있으나, 기본적으로는 라디안은 단위가 아니라 하나의 기호로 생각하시면 될듯 합니다. 아래 그림에서 중심각이 나타나는 각이 1라디안이 되는 것이죠. (1라디안을 실수 1과 값이 같다고 볼 수 있습니다. 예를 들어 pi 라이단이라면 실수 3.141592.. 와 같은 것입니다.)

이때 "중심각의 크기와 호의길이는 정비례한다"를 이용하면 기막힌 사실 하나를 발견할 수 있습니다. 우리는 반지름과 호의길이가 같은 부채꼴의 중심각을 1라디안으로 정의했습니다. 이를 반대로 말하면, 중심각이 1라디안인 부채꼴의 호의 길이는 반지름과 같다. 라고 볼 수 있습니다. 이때 중심각의 크기와 호의길이는 정비례한다는 성질을 이용하면 중심각이 2라디안인 부채꼴이라면 호의길이는 반지름의 2배이며, 3라디안인 부채꼴이라면 호의길이는 반지름의 3배가 됩니다. 이를 이용하면 중심각이 2pi라디안인 부채꼴 (=원)의 호의길이가 반지름의 2pi 배가 됨을 알 수 있습니다. 자연스럽게 원의 둘레의 길이 공식이 다시금 확인됩니다. 이를 정리하면 아래 그림과 같습니다.

이는 부채꼴에서 중심각이 호의길이에 정비례함을 이용한 것이고, 부채꼴의 넓이 또한 중심각과 비례관계에 있으므로 다음과 같은 부채꼴의 호의길이/넓이 공식을 유도할 수 있습니다.
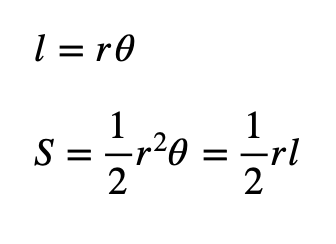
결국, 위 공식을 쓸 수 있는 이유는 우리가 "호도법"을 창안했기 때문이기에 중심각이 각도 단위일 때는 위 공식을 쓸 수 없습니다. 따라서, 부채꼴의 중심각이 각도단위로 되어 있다면 이를 라디안 단위로 바꾸어 공식을 적용해야 합니다.
② 호도법 예제

혹시 답으로 30이 나오셨다면, 반성해야합니다. 이는 '도' 단위와 '라디안'을 구분하지 않고 무분별하게 공식만을 적용했기 때문에 발생한 오류입니다. 아래 해설을 보시고, 그럼에도 이해가 안되신다면 교과서나 개념 교재를 다시 한번 읽어보시기 바랍니다. 물론, 글 상단에 있는 연락처로 저에게 질문하셔도 됩니다. 이제 동경에 대해 배워보도록 하겠습니다.

③ 동경의 정의
우리는 앞서 "호도법"이라는 새로운 각 표현 도구에 대해 배웠습니다. 호도법의 장점은 각도를 실수의 개념으로 해석할 수 있음이었고 나아가 "삼각함수의 그래프"에서 정의역을 실수로 표현할 수 있게 되었습니다. 본격적으로 삼각함수의 정의를 배우기 이전에, 동경이라는 새로운 정의를 알아보고 가겠습니다. 동경이라 함은 기본적으로 "반직선"이며, 시초선이라는 또 다른 "반직선"과의 끼인각의 크기를 비로소 삼각함수의 각으로서 정의하게 됩니다. 이처럼 앞으로 "각의 크기"는 "동경"과 뗄 수 없는 존재로서, "동경"을 "각의 크기"를 나타내는 반직선으로서 이해하면 될 것 같습니다.

(2) 삼각함수의 정의
① 삼각함수의 정의
이제 본격적으로 삼각함수의 정의에 대해 알아보곘습니다. 기본적으로 삼각함수의 정의에는 "원"과 "각을 나타내는 동경" 두가지만 있으면 됩니다. 따라서, 아래와 같은 상황에서 sin / cos / tan 를 정의하게 됩니다.
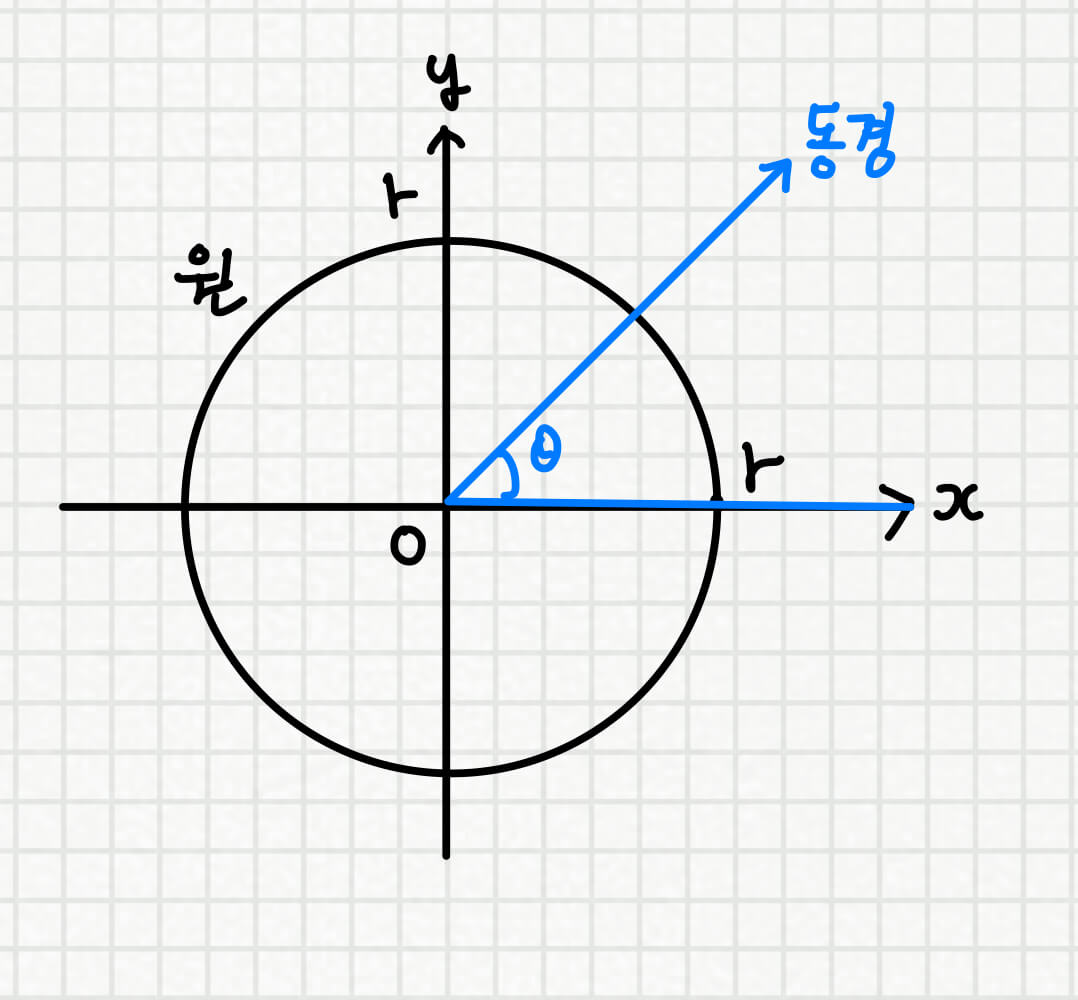
우리는 삼각비가 직각삼각형과 관련있음을 중학교 때 배웠습니다. 따라서 우리는 동경과 원의 교점을 P라고 할 때, OP를 빗변으로 하는 직각삼각형을 그릴 수 있으며 해당 직각삼각형을 이용하여 sin / cos / tan에 대해 정의하게 됩니다.
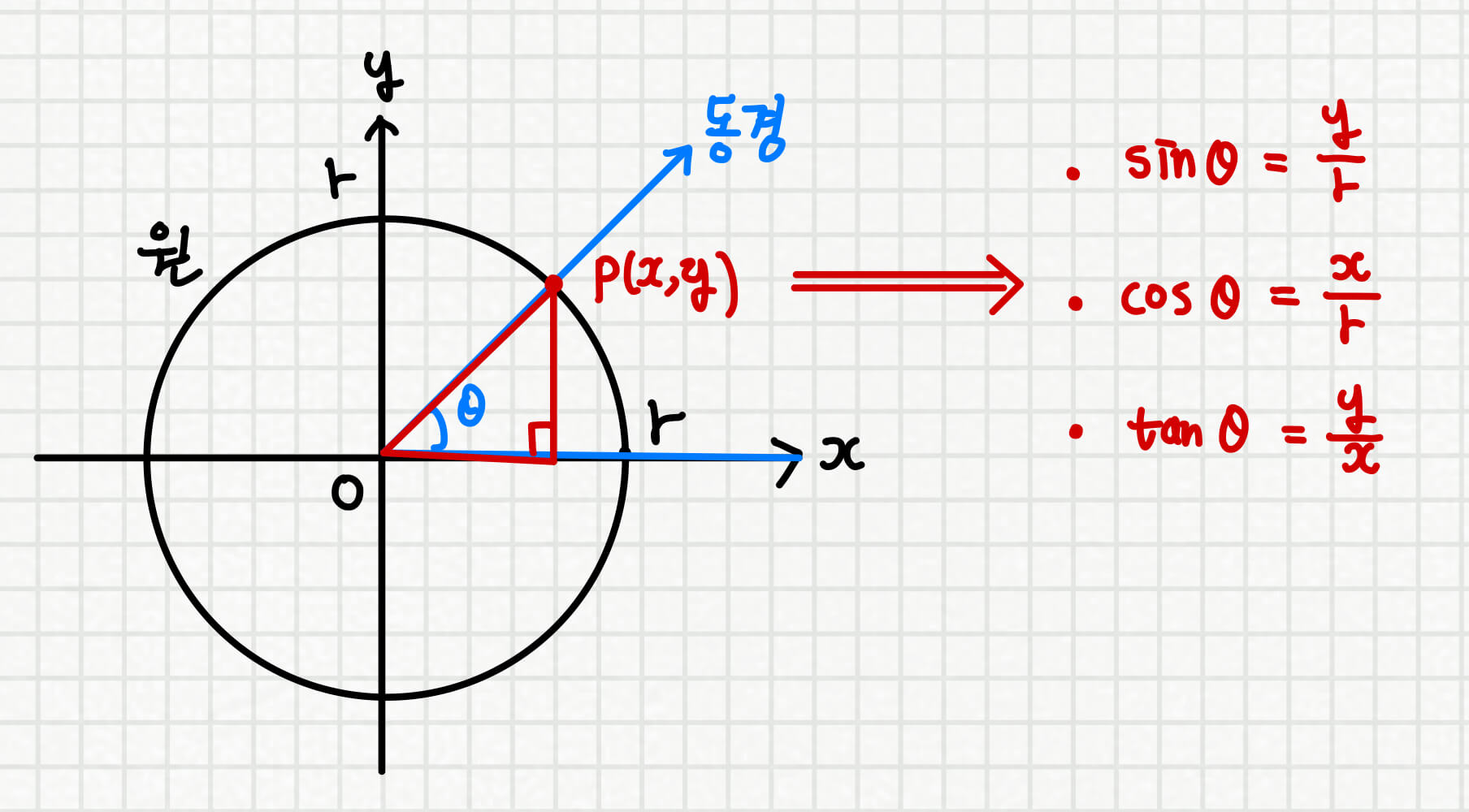
즉, 수학자들은 원과 동경의 교점인 P의 x좌표, y좌표가 sin / cos / tan 를 나타내도록 정의하였습니다. 이를 이용하여, 제 1사분면 / 제 2사분면 / 제 3사분면 / 제 4사분면 에서의 sin / cos / tan 의 부호가 결정된 것입니다. 예를 들어, 3사분면에서는 x좌표와 y좌표 모두 음수이므로 sin과 cos은 음의 값을 가지게 되고 tan는 양의 값을 가지게 됩니다. (*반지름은 항상 양수로 취급합니다)
조금 더 확장해서 생각해볼 때 만약 반지름이 1인 원에 대하여 위의 삼각함수 정의를 적용하면 어떻게 될까요? 그렇습니다. sin은 P의 y좌표를, cos은 P의 x좌표를, tan는 P와 원점 사이의 기울기를 나타내게 됩니다. 이 사실이 맨 처음 우리가 본 대표문제 풀이의 핵심아이디어가 됩니다. 이는 마지막에 다시한번 살펴보도록 합시다.
② 삼각함수의 정의에 따른 성질
우리는 삼각함수를 원과 동경의 교점으로 정의했기 때문에 아래와 같은 두가지 성질을 얻을 수 있습니다. 첫번째 성질은 sin과 cos의 관계에 대한 식입니다. 이는 점 P가 반지름이 r인 원 위의 점이기 때문에 점 P의 (x좌표 제곱) + (y좌표 제곱) = (r 제곱)을 이용한 식입니다. 또한 두번째 성질의 경우 sin / cos / tan 의 정의를 이용하면 손쉽게 증명할 수 있습니다.

3. 문제 풀이
본격적으로 대표문제를 풀기 앞서, 삼각함수의 정의를 활용한 의미있는 문제 하나만 보고 가겠습니다.
(1) 예제 풀이

① 조건 해석
먼저, 원과 각이 등장했으므로 삼각함수의 정의를 떠올려야 하는 문제입니다. 삼각함수를 정의할 때, 우리는 원과 동경의 교점인 P를 중심으로 삼각함수를 정의했으므로 위 문제에서 원과 동경의 교점을 찾아야 합니다. 그러나, 원이 2개 존재하므로 교점 또한 각 하나당 두개씩 존재하게 됩니다. 그러므로 어떤 교점을 이용해 문제를 해결할지가 문제풀이의 핵심이 되는 문제이며 y = 2 라는 직선이 교점의 y좌표를 알려줌을 발견했다면, 두 점중 어떤 점을 교점으로 봐야하는 손쉽게 알 수 있었을 것입니다.
② 모범 답안
따라서, 아래와 같이 알파와 베타에 대한 "sin"값을 구할 수 있게 됩니다. (교점의 y좌표를 주었으므로, cos의 정의를 이용할 수 있다.)


이때, 삼각함수의 정의를 이용하여 문제에서 구하라고 한 값을 구하면 됩니다. (*TIP 각이 같은 상황에서 sin값을 이용해 cos값(혹은 tan값)을 구할 때는 직각삼각형을 그린 뒤 부호만 주의해주면 됩니다.)

(2) 대표문제 풀이

① 조건 해석
위의 예제 문제와 마찬가지로, 원과 각이 등장하므로 삼각함수의 정의를 떠올려야 합니다. 그런데, 해당 원이 단순한 원이 아니라 반지름의 길이가 1인 단위원 이므로 해당 원에서 정의된 삼가함수들은 각각 sin은 P의 y좌표를, cos은 P의 x좌표를, tan는 P와 원점 사이의 기울기를 의미하게 됩니다. 이를 이용하면 문제를 손쉽게 해결할 수 있습니다.
② 모범 답안
먼저 sin값들의 합을 구해보면, sin은 교점 P의 y좌표로서 정의됩니다. 이때 sin(1 세타)는 P1에 대응되고 sin(2 세타)는 P2에 대응되며 ... 쭉 나아가 sin(10세타)는 P10에 대응됩니다. 이때 sin은 교점 P의 y좌표를 의미하므로 아래와 같은 그림을 머릿속으로 생각했을 때, sin값들의 총합은 0이 됩니다.
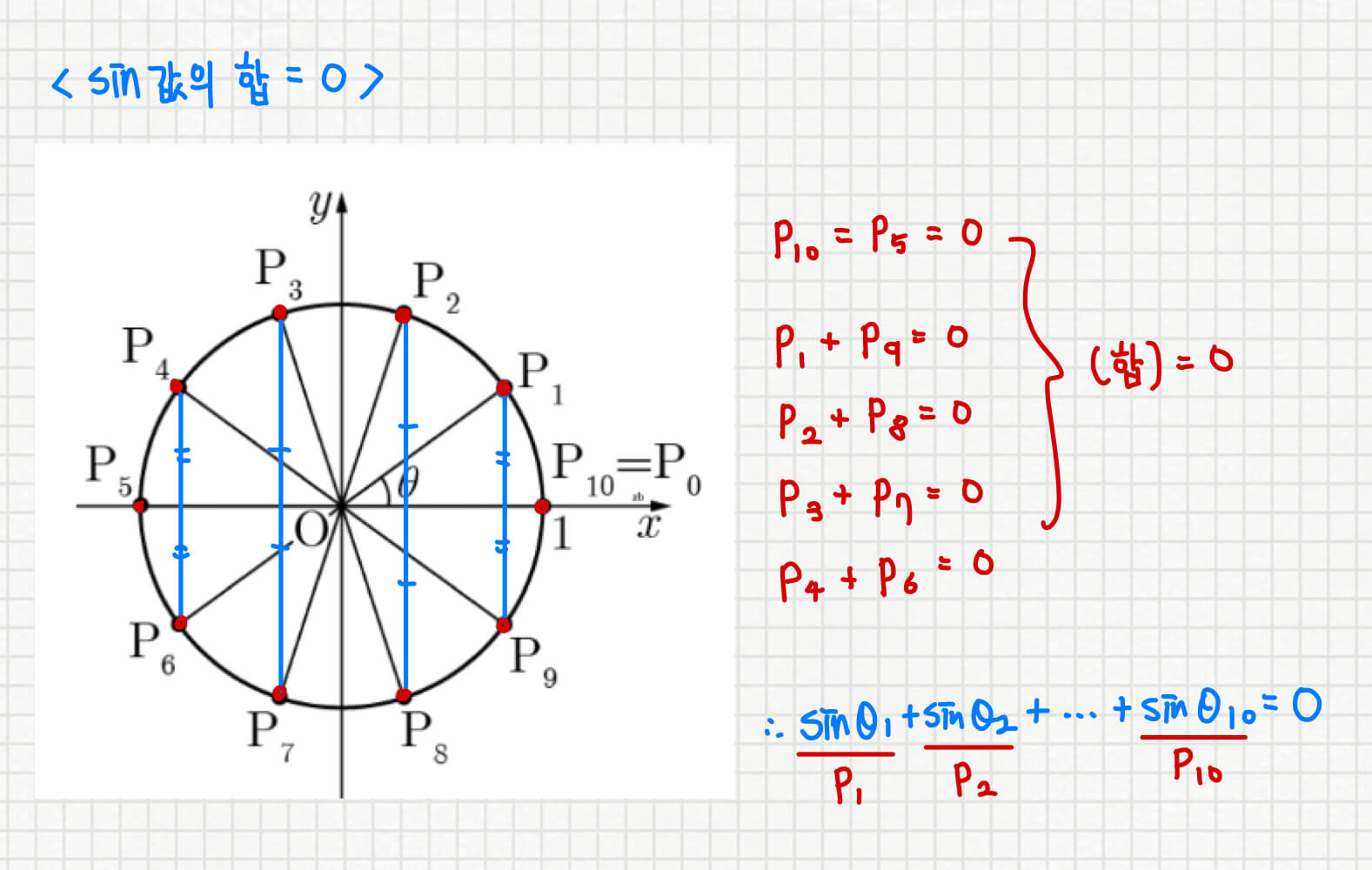
이후 cos값들의 합을 구해보면, cos은 교점 P의 x좌표로서 정의됩니다. 이때 cos(1 세타)는 P1에 대응되고 cos(2 세타)는 P2에 대응되며 ... 쭉 나아가 cos(10세타)는 P10에 대응됩니다. 이때 cos은 교점 P의 x좌표를 의미하므로 아래와 같은 그림을 머릿속으로 생각했을 때, cos값들의 총합은 0이 됩니다.

마지막으로 tan값들의 합을 구해보면, cos은 교점 P와 원점의 기울기로서 정의됩니다. 이때 tan(1 세타)는 P1에 대응되고 tan(2 세타)는 P2에 대응되며 ... 쭉 나아가 tan(10세타)는 P10에 대응됩니다. 이때 cos은 교점 P와 원점의 기울기를 의미하므로 아래와 같은 그림을 머릿속으로 생각했을 때, tan값들의 총합은 0이 됩니다.

따라서, 문제의 답은 0 + 0 + 0 = 0 이 됩니다.
오늘은 <삼각함수의 정의>에 대하여 같이 공부해보았습니다. 다음 시간에는 오늘 배운 "삼각함수의 정의"를 이용하여 시험에 최소 1문제씩 꼭 나오는 <삼각함수의 계산>에 대하여 공부하도록 하겠습니다.
'밤샘수학 > 수학1 실전 개념' 카테고리의 다른 글
| [수학 1 실전 개념] 15강 : 삼각함수의 각변환 <예각가정법> (0) | 2023.04.15 |
|---|---|
| [수학 1 실전 개념] 13강 : 지수/로그 실생활 활용 - 유형(2) (0) | 2023.04.04 |
| [수학 1 실전 개념] 12강 : 지수/로그 실생활 활용 - 유형(1) (0) | 2023.04.04 |
| [수학 1 실전 개념] 11강 : 지수 방부등식 - 치환 (범위에 유의하기) (0) | 2023.04.04 |
| [수학 1 실전 개념] 10강 : 지수/로그 함수 그래프 (5) - 스킬) 추론형 문제 - 대소관계 (0) | 2023.04.04 |
댓글
이 글 공유하기
다른 글
-
[수학 1 실전 개념] 15강 : 삼각함수의 각변환 <예각가정법>
[수학 1 실전 개념] 15강 : 삼각함수의 각변환 <예각가정법>
2023.04.15 -
[수학 1 실전 개념] 13강 : 지수/로그 실생활 활용 - 유형(2)
[수학 1 실전 개념] 13강 : 지수/로그 실생활 활용 - 유형(2)
2023.04.04 -
[수학 1 실전 개념] 12강 : 지수/로그 실생활 활용 - 유형(1)
[수학 1 실전 개념] 12강 : 지수/로그 실생활 활용 - 유형(1)
2023.04.04 -
[수학 1 실전 개념] 11강 : 지수 방부등식 - 치환 (범위에 유의하기)
[수학 1 실전 개념] 11강 : 지수 방부등식 - 치환 (범위에 유의하기)
2023.04.04