[2023년 3월 모의고사 - 고3] 공통 후반부 (16번~22번) 해설 - 요약

2023 3월 모의고사 공통 16번

 [핵심 key Point]

 => 로그의 성질을 이용한 단순 계산

 

 [자세한 해설]

 => 생략

 

2023 3월 모의고사 공통 17번

 [핵심 key Point]

 => 접선의 방정식

 

 [자세한 해설]

 => 접점의 x좌표를 t라 두고, 함숫값과 미분값이 같음을 이용

 

2023 3월 모의고사 공통 18번

 [핵심 key Point]

 => 수열의 합 공식

 

 [자세한 해설]

 => 인수 분해 혹은 근과 계수의 관계를 적용하여 계산한다.

 

2023 3월 모의고사 공통 19번

 [핵심 key Point]

 => 속도의 부정적분은 위치이다.

 

 [자세한 해설]

 => 원점에서 출발하므로 적분상수는 0!

 => 이후, 차의 함수를 이용했을 때 (일차)*(이차)로 인수분해 되며

      이때 이차식이 중근을 가져야 한 점에서 만난다.

 

2023 3월 모의고사 공통 20번

 [핵심 key Point]

 => 삼차함수의 그래프 해석 + 평행이동

 

 [자세한 해설]

 => (가) 조건을 (나) 조건에 대입하면 함수 f(x)가 x=p, x=-p 에서 극값을 가짐을 알 수 있다

 => 이후 정적분값이 20임을 이용하면, p 값을 구할 수 있다.

 

2023 3월 모의고사 공통 21번

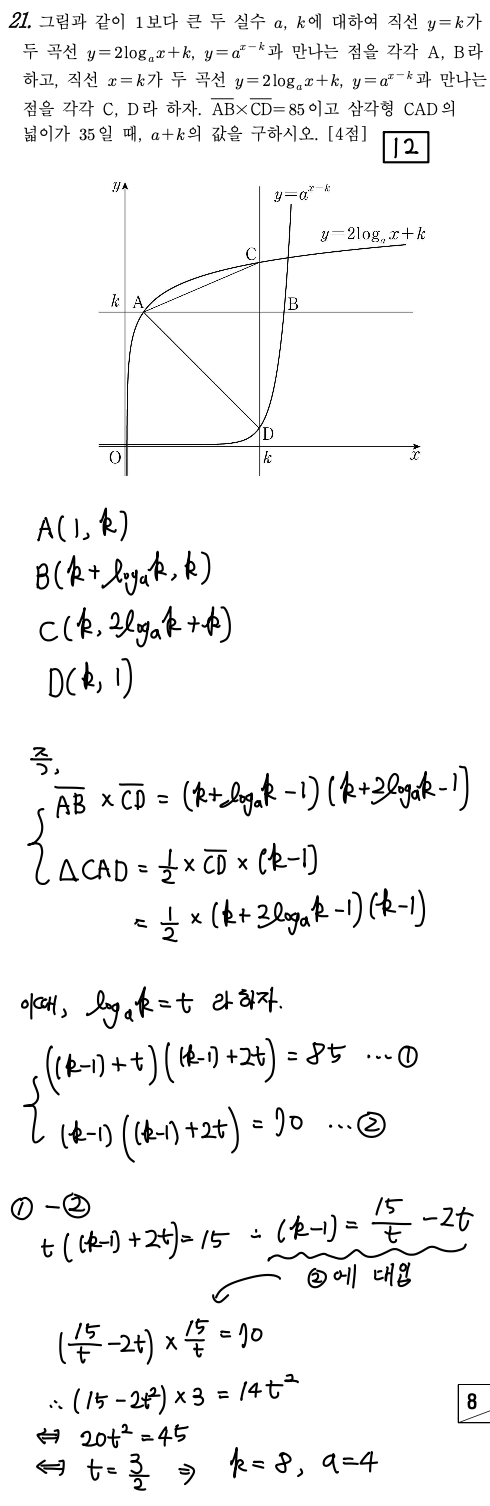
 [핵심 key Point]

 => 복잡한 로그 방정식의 연립

 

 [자세한 해설]

 => A, B, C, D 모두 좌표값을 a, k에 대해 나타낸다.

 => 문제에서 준 조건 2가지로 연립식을 세운 뒤 로그값을 t로 치환한다.

 

2023 3월 모의고사 공통 22번

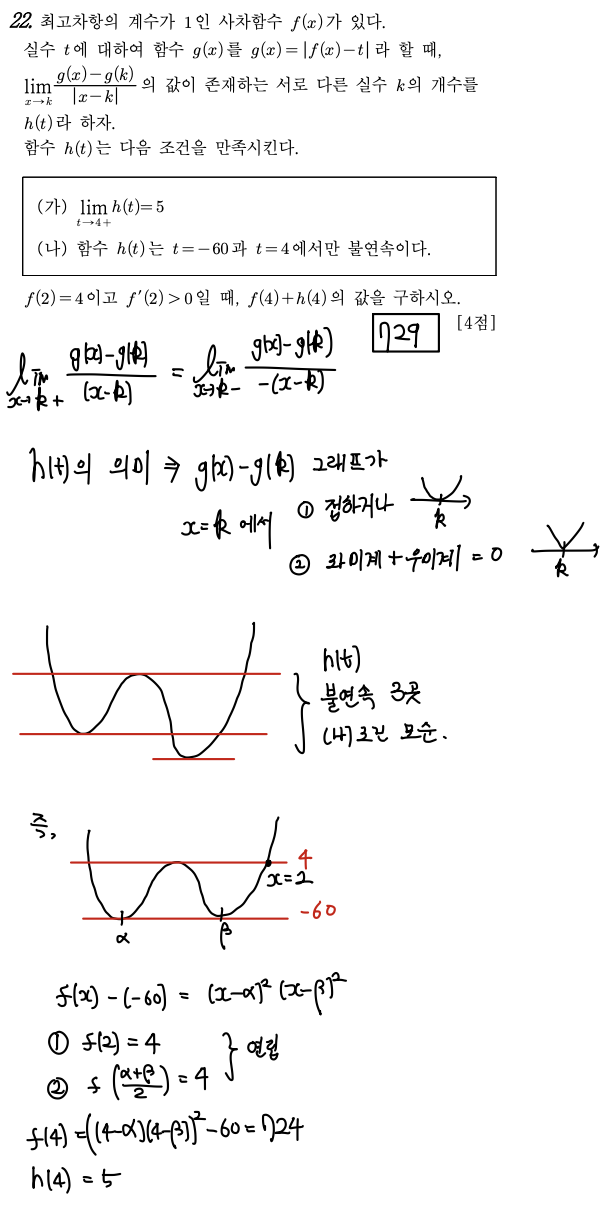
 [핵심 key Point]

 => 사차함수의 그래프 해석

 

 [자세한 해설]

 => h(t)의 의미를 파악하는 것이 무엇보다 중요한 문제이다.

 => 직관적으로 g(x)-g(k) 가 (x-k) 인수를 2개 가져야 함을 알 수 있고,

      절댓값 기호를 풀어주면, g(x)-g(k) 가 (x-k) 인수 1개 + (x=k에서, 좌미계 + 우미계 = 0) 일 때도 성립함을 알 수 있다.

 => 또한, 불연속인 점이 2개만 존재하려면, 극댓값이 4가 되야하고 극솟값 2개 모두 -60 이 되어야 한다.

      이후 차의 함수를 이용해 f(x)-(-60)을 α와 β로 나타낸 뒤 연립하면 된다.