[2023년 3월 모의고사 - 고3] 공통 전반부(1번~15번) 해설 - 요약
2023 3월 모의고사 공통 1번

[핵심 key Point]
=> 지수 법칙을 이용한 단순 계산
[자세한 해설]
=> 생략
2023 3월 모의고사 공통 2번

[핵심 key Point]
=> 다항함수의 미분법을 이용한 단순 계산
[자세한 해설]
=> 생략
2023 3월 모의고사 공통 3번

[핵심 key Point]
=> 등비수열의 일반항
[자세한 해설]
=> 초항과 공비를 둘다 미지수로 잡고 연립하는 것 보다,
주어진 5번째 항의 값과 공비를 이용하여 다른항을 표현해야 계산을 줄일 수 있다.
2023 3월 모의고사 공통 4번

[핵심 key Point]
=> 부정적분은 미분하고 대입하고 관찰한다.
[자세한 해설]
=> 당연히 x=1 을 대입하고, 양변을 미분해야 한다.
2023 3월 모의고사 공통 5번

[핵심 key Point]
=> 삼각함수의 정의 + 사분면에 따른 부호 주의
[자세한 해설]
=> 삼각함수를 간단히 표현하고, 각이 제 3사분면임을 파악하는 것이 중요하다.
2023 3월 모의고사 공통 6번

[핵심 key Point]
=> 연속의 정의
[자세한 해설]
=> 좌극한과 우극한이 같음을 이용
2023 3월 모의고사 공통 7번

[핵심 key Point]
=> 이차함수의 정적분 공식
[자세한 해설]
=> 그저 정적분 식을 쓰는 것 보다, 구하고자 하는 넓이를
(직사각형)+(공식을 쓸수 있는 넓이)로 쪼개면 계산이 간편하다.
2023 3월 모의고사 공통 8번

[핵심 key Point]
=> 로그 방정식
[자세한 해설]
=> 내분점 공식을 까먹지 않았다면, 로그 방정식을 잘 풀기만 하면 된다.
2023 3월 모의고사 공통 9번
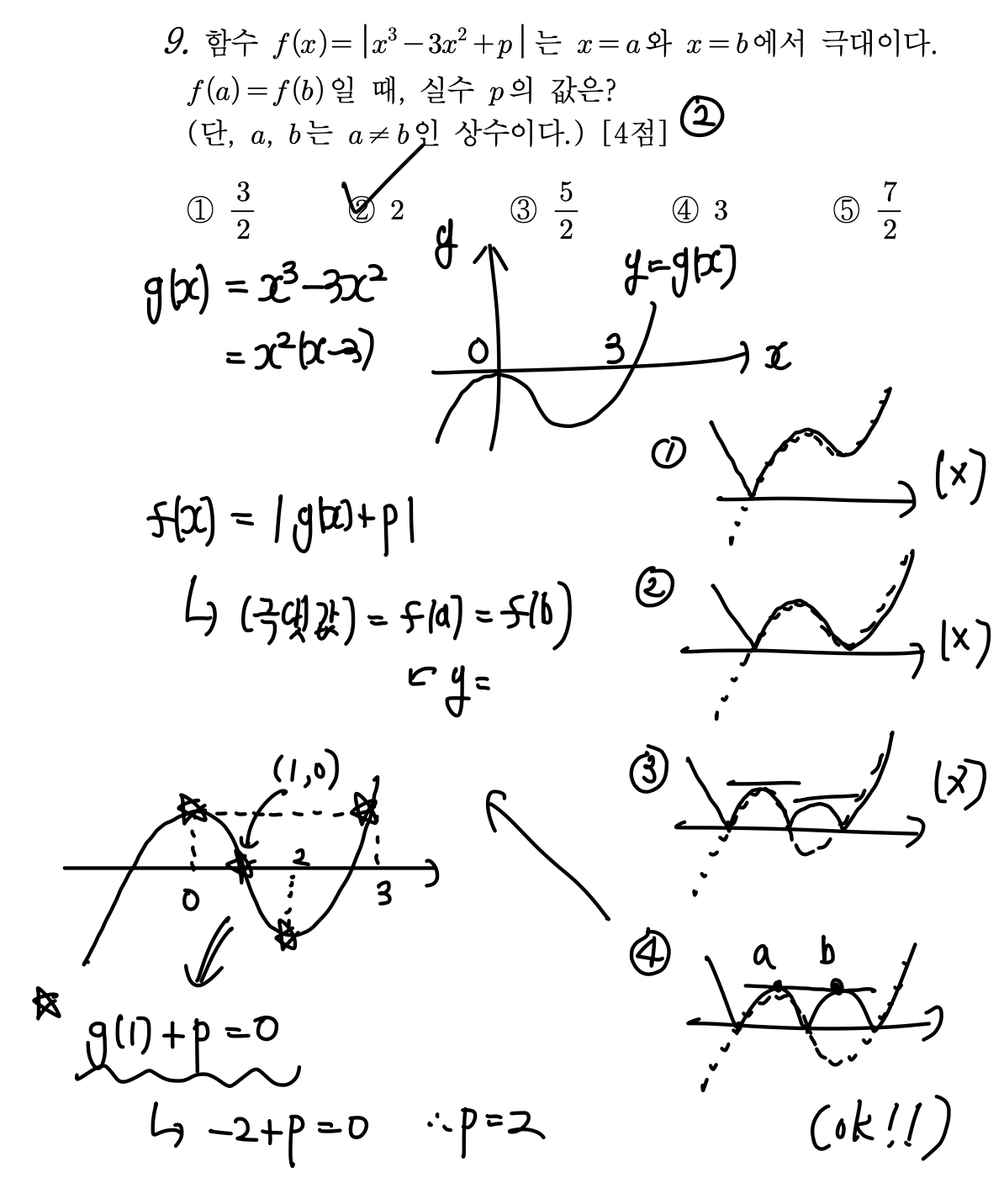
[핵심 key Point]
=> 절댓값이 있는 삼차함수의 그래프 해석
[자세한 해설]
=> 먼저 g(x) = x^3-3x^2 그래프를 그린 뒤, y축으로 평행이동해가며 그 형태를 관찰한다.
그때, 극댓값이 2개 존재하며 그 값이 같으려면 매우 특수한 경우임을 인지해야 한다.
g(x) + p 의 그래프의 극대/극소가 서로 절댓값은 같고 부호만 반대임을 파악했다면
삼차함수의 다섯개의 특수한 점을 그래프에 찍었을 때, y = g(x) + p 그래프가 (1, 0)을 지나야 한다.
2023 3월 모의고사 공통 10번
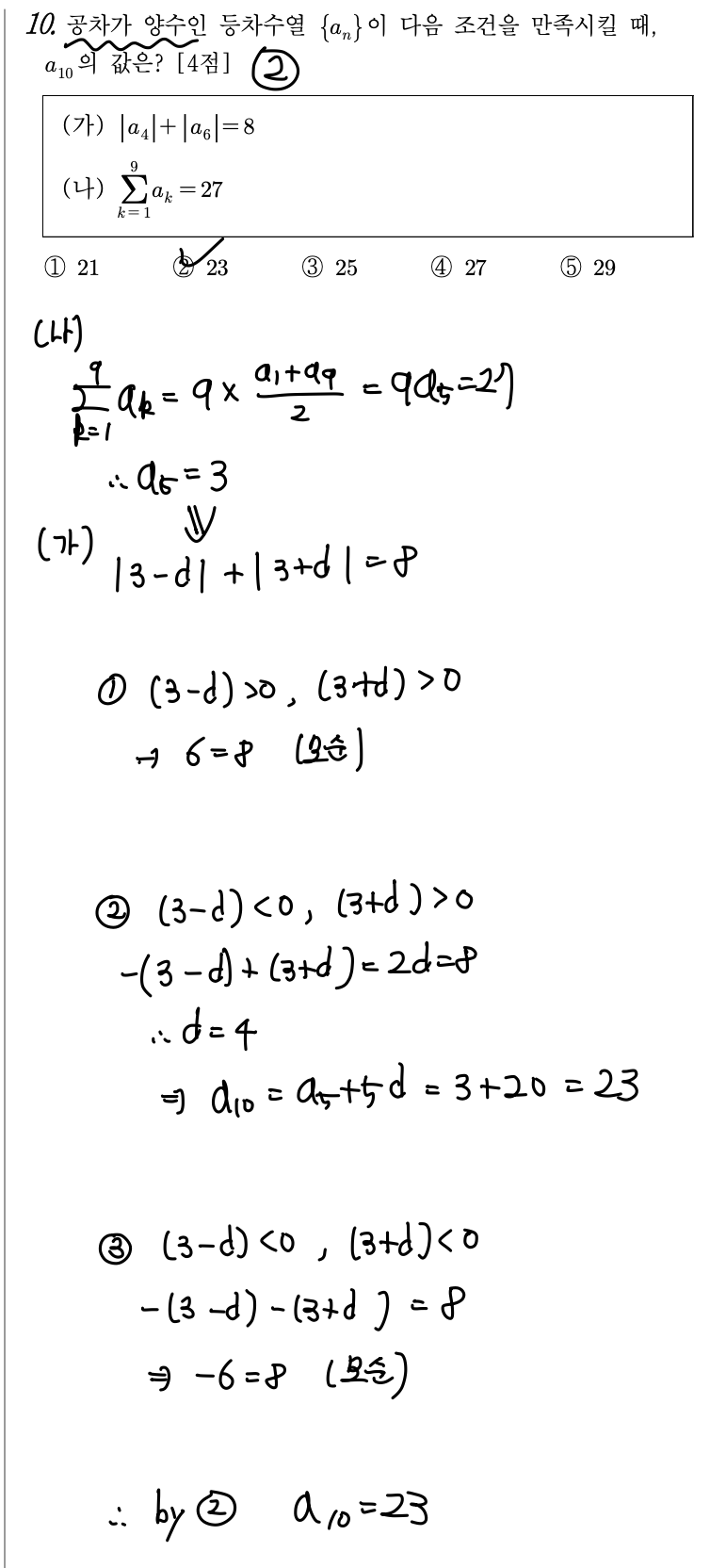
[핵심 key Point]
=> 등차수열의 합은 평균 * 개수 이다.
[자세한 해설]
=> (나) 조건을 먼저 해석하면, 5번째 항의 값이 3임을 알 수 있다.
이후, (가) 조건에서 (3-d)와 (3+d)의 부호에 따른 경우를 3가지로 나눈 뒤
조건을 써보면 답이 나오는 경우는 1가지 뿐이다.
2023 3월 모의고사 공통 11번
[
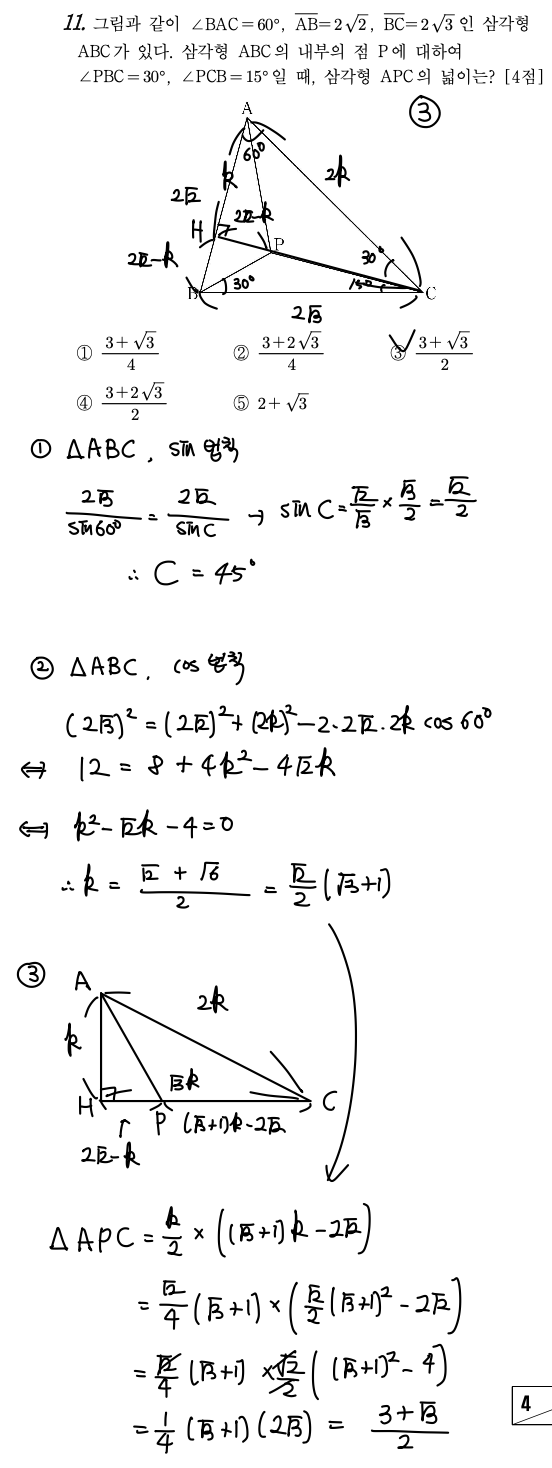
핵심 key Point]
=> sin 법칙과 cos 법칙을 통한 특수각의 발견, 복잡한 계산 마무리
[자세한 해설]
=> 먼저 △ABC에 sin 법칙을 적용하면 각C의 크기가 45도 임을 알 수 있고.
이를 이용하면 직선 CP가 선분 AB와 수직임을 알 수 있다.
이때 수선의 발을 H라 하면, △ACH와 △CDH는 모두 직각삼각형이 된다.
=> 따라서, AC의 길이를 2k라 두고 표현할 수 있는 모든 길이를 k에 대하여 표현한다.
이후 다시 △ABC에 cos 법칙을 적용하면 k값을 구할 수 있고,
=> △APC의 넓이도 구할 수 있다.
2023 3월 모의고사 공통 12번
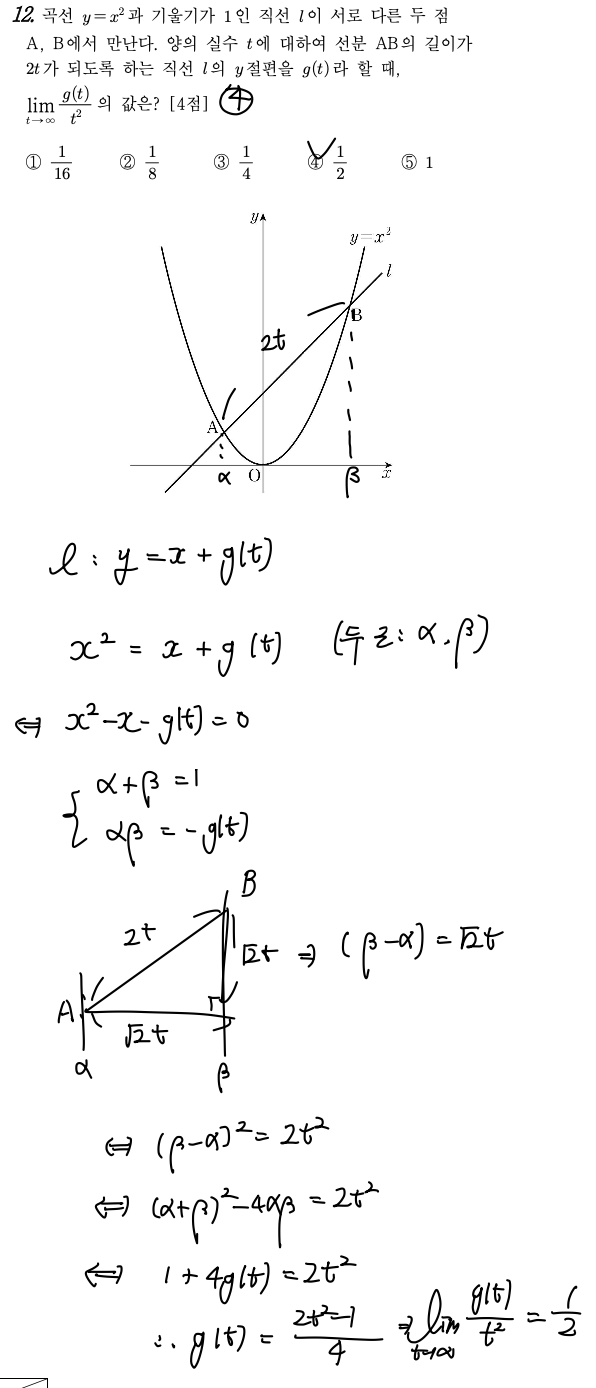
[핵심 key Point]
=> 극한식의 활용
[자세한 해설]
=> 생략
2023 3월 모의고사 공통 13번

[핵심 key Point]
=> 합성함수의 근을 해석하는 방법
[자세한 해설]
=> (가) 조건에 의하여 a는 1/2 또는 3/2 가 된다.
=> (나) 조건에서, f(x)가 최대 두근을 가지므로 각각의 근을 α와 β로 가정한다.
즉, (g(x) = α의 근의 합) + (g(x) = β의 근의 합) = (5/2)ㅠ
=> 따라서, g(x) = (어떤 상수) 의 근의 합을 ①, ②, ③, ④, ⑤경우로 나누어 생각한다.
이때 ② + ⑤ 의 값이 정확히 (5/2)ㅠ 이므로 0 < α < 1 , β = -1 임을 알 수 있다.
=> (가) 조건에 의한 a 두 값을 경우 나누어 대입하면, 답을 구할 수 있다.
2023 3월 모의고사 공통 14번
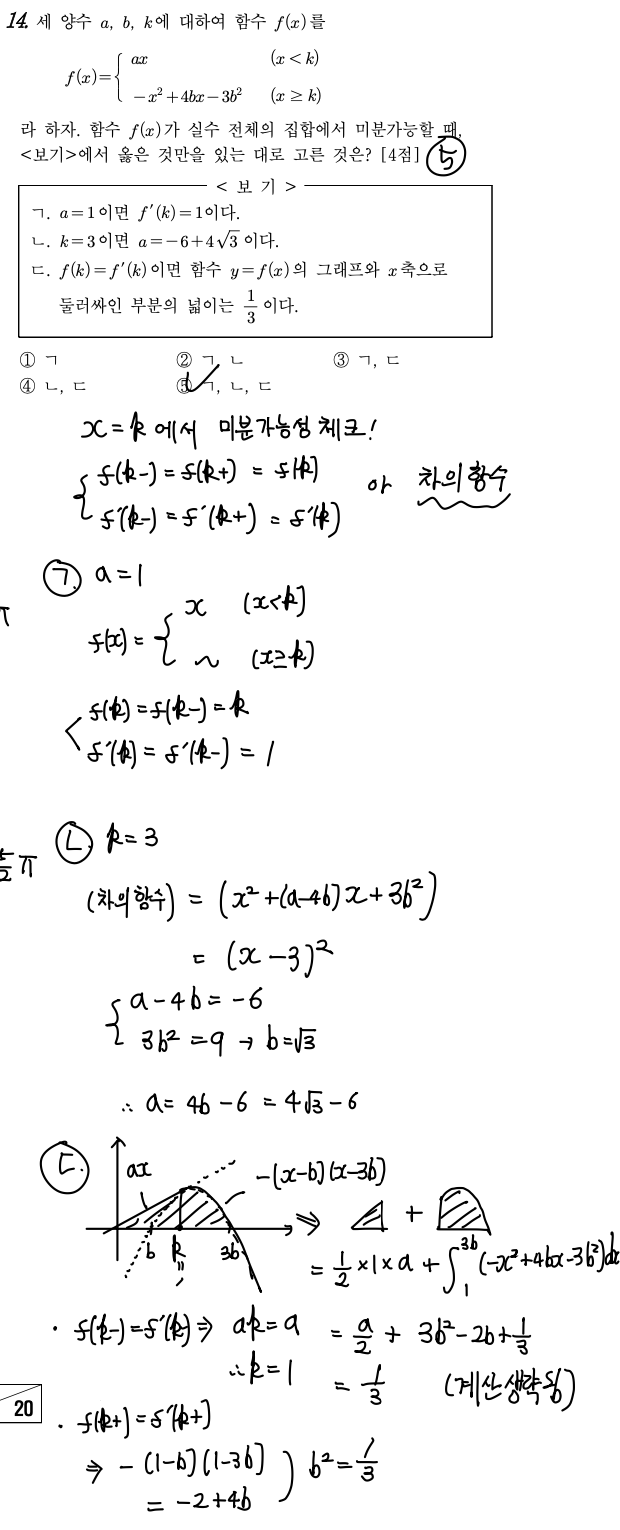
[핵심 key Point]
=> 구간으로 정의된 함수의 미분가능성 판단
[자세한 해설]
=> ㄱ. 좌극한=우극한 / 좌미분계수=우미분계수
=> ㄴ. 차의 함수가 완전 제곱꼴이어야 함을 이용
=> ㄷ. 복잡한 계산
2023 3월 모의고사 공통 15번

[핵심 key Point]
=> 짝 홀 케이스 나누기
[자세한 해설]
=> 생략 (그림 참고)
'밤샘수학 > 기출 해설' 카테고리의 다른 글
| [2024학년도 수능 - 2023년 시행] 수학 예상 등급컷&총평 / 손글씨 해설(1번-15번) (1) | 2023.11.16 |
|---|---|
| [2023년 3월 모의고사 - 고3] 공통 후반부 (16번~22번) 해설 - 요약 (0) | 2023.03.23 |
댓글
이 글 공유하기
다른 글
-
[2024학년도 수능 - 2023년 시행] 수학 예상 등급컷&총평 / 손글씨 해설(1번-15번)
[2024학년도 수능 - 2023년 시행] 수학 예상 등급컷&총평 / 손글씨 해설(1번-15번)
2023.11.16인사의 말 2024 수능을 끝낸 수험생 모두들 고생 많았습니다. 이번 2024 수능의 전체적인 난이도와 예상 등급컷 그리고 해설 강의를 시작하겠습니다. 올해 수험생에겐 마지막으로 정리하는 마음으로, 내년 수험생에겐 전년도 수능의 분석 글로 활용해주면 좋을 것 같습니다. 자 그럼 2024 수능 총평부터 바로 들어가겠습니다. 전체적인 문항별 난이도 및 예상 등급컷 (공통) 1번-8번 (2, 3점) : 매우 쉬움. 다만, 8번에서 기함수/우함수 성질 안쓰면 계산 조금 복잡한 정도?) 9번-10번 (쉬운 4점) : 9번에서 로그 성질 깔끔하게 써주고, 10번은 절댓값에 주의만 해주었으면 4등급 이상 학생들은 무난하게 풀었을 난이도. 11번-15번 (준킬러 4점) : 6, 9모 11번-15번의 난이도 보다 전체적… -
[2023년 3월 모의고사 - 고3] 공통 후반부 (16번~22번) 해설 - 요약
[2023년 3월 모의고사 - 고3] 공통 후반부 (16번~22번) 해설 - 요약
2023.03.232023 3월 모의고사 공통 16번 [핵심 key Point] => 로그의 성질을 이용한 단순 계산 [자세한 해설] => 생략 2023 3월 모의고사 공통 17번 [핵심 key Point] => 접선의 방정식 [자세한 해설] => 접점의 x좌표를 t라 두고, 함숫값과 미분값이 같음을 이용 2023 3월 모의고사 공통 18번 [핵심 key Point] => 수열의 합 공식 [자세한 해설] => 인수 분해 혹은 근과 계수의 관계를 적용하여 계산한다. 2023 3월 모의고사 공통 19번 [핵심 key Point] => 속도의 부정적분은 위치이다. [자세한 해설] => 원점에서 출발하므로 적분상수는 0! => 이후, 차의 함수를 이용했을 때 (일차)*(이차)로 인수분해 되며 이때 이차식이 중근을 가져야 한 점에…
댓글을 사용할 수 없습니다.