[2024학년도 수능 - 2023년 시행] 수학 예상 등급컷&총평 / 손글씨 해설(1번-15번)
인사의 말
2024 수능을 끝낸 수험생 모두들 고생 많았습니다.
이번 2024 수능의 전체적인 난이도와 예상 등급컷 그리고 해설 강의를 시작하겠습니다.
올해 수험생에겐 마지막으로 정리하는 마음으로, 내년 수험생에겐 전년도 수능의 분석 글로 활용해주면 좋을 것 같습니다.
자 그럼 2024 수능 총평부터 바로 들어가겠습니다.
전체적인 문항별 난이도 및 예상 등급컷
(공통)
1번-8번 (2, 3점)
: 매우 쉬움. 다만, 8번에서 기함수/우함수 성질 안쓰면 계산 조금 복잡한 정도?)
9번-10번 (쉬운 4점)
: 9번에서 로그 성질 깔끔하게 써주고, 10번은 절댓값에 주의만 해주었으면 4등급 이상 학생들은 무난하게 풀었을 난이도.
11번-15번 (준킬러 4점)
: 6, 9모 11번-15번의 난이도 보다 전체적으로 쉬워짐. 대신 계산량을 조금 늘린 느낌이고 특히 15번의 경우
그 동안 기출에서 보인 수열 킬러 문제의 형태를 띠고 있으나 난이도는 그에 비해 훨씬 쉬움.
1등급 안정권 학생의 경우 5문제 중에서 틀린 문제가 있으면 안됨.
2등급의 경우 1문제 정도, 3등급의 경우 2문제 정도 틀릴만한 난이도.
16번-19번 (3점)
: 매우 쉬움
20번-22번 (준킬러 4점)
: 22번은 킬러의 역할을 해주었을 것이고, 20번은 계산 파티에 21번은 그래프만 잘 그려주면 무난했을 난이도.
(난이도 : 22번 > 20번 > 21번)
22번은 틀려도 1등급 가능할듯.
(선택-미적분)
23번-26번 (2, 3점)
: 쉬움. 다만, 25번의 경우 역함수 -> 치환적분 쓸 생각을 하지 못했다면 풀기 어려웠을 것.
27번 (어려운 3점)
: 2024 9모 30번과 유사한 문제. 우함수의 미분법과 변수 구분을 잘 해주면 3등급 이상 학생은 무난하게 풀었을 것.
28번-30번 (준킬러 4점)
: 28, 30번의 경우 계산량은 그리 많지 않으나 아이디어가 어려움. 29번 아이디어의 경우 그간의 기출로 잘 알려져 있으나 계산량이 많으며 마지막 답을 구하는 과정에서 당황했을 가능성 존재. 따라서 28, 30번이 1등급을 가르는 문제로서, 29번이 2등급을 가르는 문제로 작용했을 것으로 예상됨.
공통 22번과 미적 28, 30번 3개만 딱 틀린 88점이 1등급컷으로 예상됨.
(선택-확통)
제작중
(예상 미적 등급컷)
1등급 : 84~88
2등급 : 72~76
3등급 : 64~68
공통 문항별 분석 및 손글씨 해설
[2024학년도 수능 수학 1번]
유형 : 수1 - 거듭제곱근과 지수법칙
분석 : 생략
[2024학년도 수능 수학 2번]
유형 : 수2 - 미분계수의 정의
분석 : 생략
[2024학년도 수능 수학 3번]
유형 : 수1 - 삼각함수의 계산
분석 : 생략
[2024학년도 수능 수학 4번]
유형 : 수2 - 함수의 연속
분석 : 생략
[2024학년도 수능 수학 5번]
유형 : 수2 - 부정적분의 정의
분석 : 생략
[2024학년도 수능 수학 6번]
유형 : 수1 - 등비수열
분석 : 등'비'수열임에 집중하여 비율로 풀면 쉬움. 물론 그냥 초항, 공비 미지수로 잡고 연립해도 비슷하긴 함.
[2024학년도 수능 수학 7번]
유형 : 수2 - 극대/극소의 정의
분석 : 혹여 극대/극소를 반대로 생각했더라도 매력적인 오답인 -8이 선지에 없으므로 대부분 잘 풀었을 것.
[2024학년도 수능 수학 8번]
유형 : 수2 - 정적분의 성질 (기함수/우함수)
분석 : 기함수/우함수 성질을 발견하지 못했더라도 그리 복잡한 계산은 아님.
[2024학년도 수능 수학 9번]
유형 : 수1 - 로그의 성질
분석 : 구하라는 답의 형태에 집중한 뒤 이를 기반으로 로그 성질을 이용하면 깔끔하게 답이 나오는 무난한 문제.
[2024학년도 수능 수학 10번]
유형 : 수2 - 정적분의 활용 (시간 속도 문제)
분석 : '거리'를 보고 '절댓값 함수'를 떠올린 뒤, 마무리 적분 또한 '절댓값'을 씌워서 해주면 무난하게 풀림.
[2024학년도 수능 수학 11번]
유형 : 수1 - 등차수열과 소거되는 시그마 형태의 혼합형 문제
분석 : 공차가 0이 아닌 조건으로 a6이 음수임을 구한 뒤 교대 수열 형태를 간단히 하고, 공차를 미지수로 잡고 이차방정식을 풀어주면 되는 무난한 계산 문제. (근 1-2년 기출의 11번 치고는 쉬운듯)
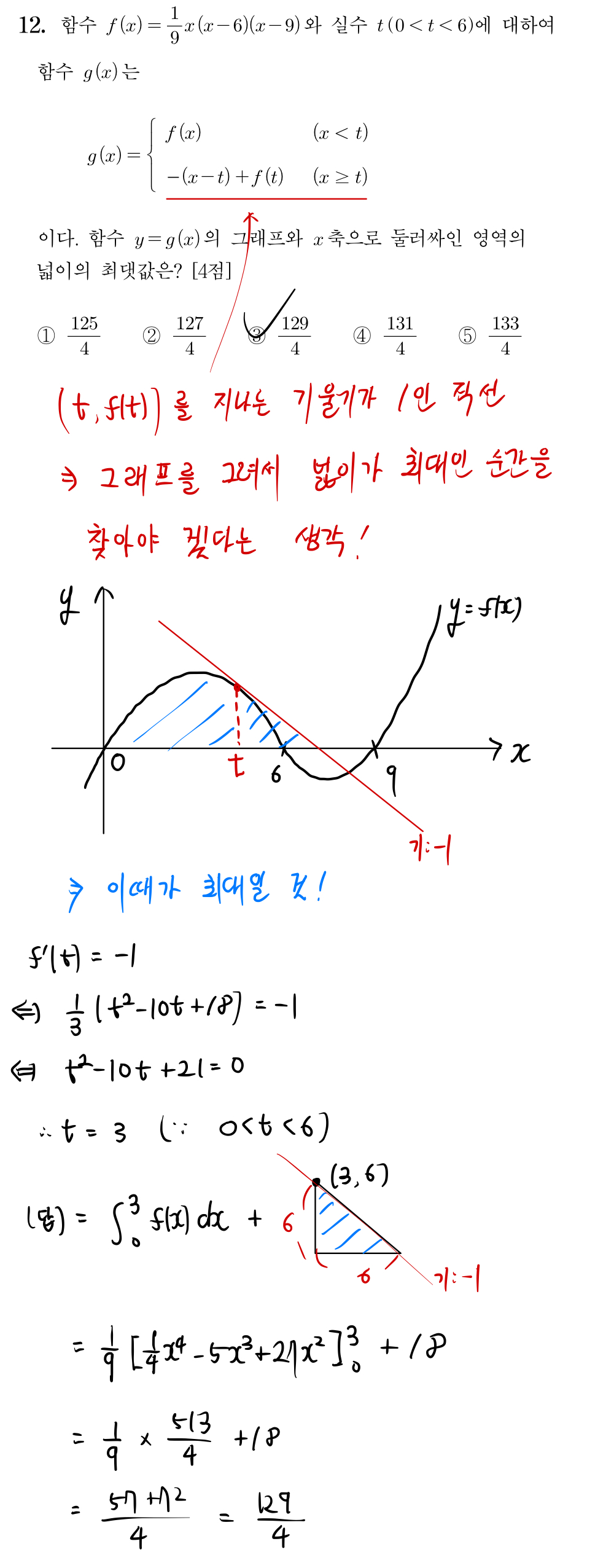
[2024학년도 수능 수학 12번]
유형 : 수2 - 다항함수의 그래프 / 미분과 정적분의 활용을 접목 시킨 문제
분석 : 넓이가 최댓값이 되도록 하는 문제 상황을 파악하는 능력이 필요하여 11번보다는 난이도가 있는 문제. 또한, 평가원스럽지 않게 계산이 복잡하여 시간 소요가 꽤 됐을 것.
[2024학년도 수능 수학 13번]
유형 : 수1 - 사인/코사인 법칙의 도형 활용 문제
분석 : 문제 조건을 따라가면 어느새 풀려있는 무난한 문제. 12번에 비해 계산도 쉽고 아이디어도 쉬운듯.
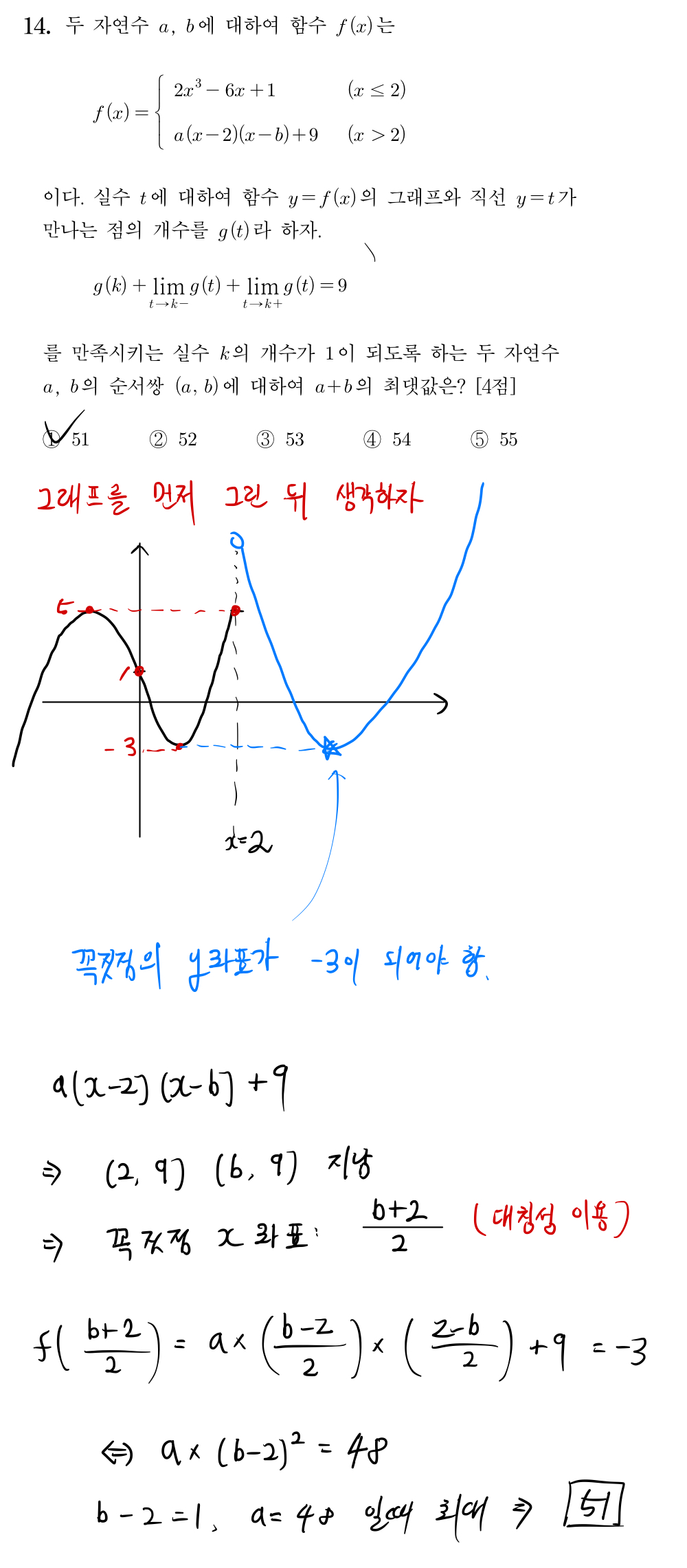
[2024학년도 수능 수학 14번]
유형 : 수2 - 함수의 극한 활용 문제
분석 : 문제 난이도는 꽤 있으나 아이디어 자체가 너무 많이 알려진 문제라 어렵지 않게 그래프를 그린 뒤 문제 조건을 만족하는 특수한 상황을 찾고 바로 풀었을듯. 물론, 마지막에 (a, b) 순서쌍을 찾는 과정에서 수학적 센스가 필요함.
[2024학년도 수능 수학 15번]
유형 : 수2 - 수열의 귀납적 정의 (=나열하며 유추하는 유형)
분석 : 수열 킬러라고 하기에는 난이도가 낮음. 잘 알려진 역추적 아이디어를 쓰는 문제. 또한, 역추적 하는 과정에서 반복되는 구조를 발견한다면 깔끔하게 풀이를 마무리할 수 있음.
'밤샘수학 > 기출 해설' 카테고리의 다른 글
| [2023년 3월 모의고사 - 고3] 공통 후반부 (16번~22번) 해설 - 요약 (0) | 2023.03.23 |
|---|---|
| [2023년 3월 모의고사 - 고3] 공통 전반부(1번~15번) 해설 - 요약 (0) | 2023.03.23 |