[기하 실전 개념 5강] 타원의 방정식 총정리

안녕하세요, 밤샘공부 입니다~
질문 사항은
아래 오픈챗 링크 혹은 메일로 보내주시면,
2시간 이내로 답변드리겠습니다.
오픈챗 링크 : https://open.kakao.com/o/srASNxef
메일 주소 : studying.all.night.1114@gmail.com
오늘도 여러분께 수학적 통찰을 주는 강의가 되었으면 합니다.
영상이 편하신 분은 아래 링크로 강의 보시면 됩니다.
영상강의 링크 : https://youtu.be/ffpAsvMXiWA
학습지 파일 링크 : https://study-all-night.tistory.com/167
[0] INTRO
본격적인 타원 강의에 앞서,
먼저 전체적인 내용을 훑어 보고 들어가겠습니다.
1. 기본 형태
*배울 내용*
가로로 긴 타원 vs 세로로 긴 타원
타원의 정의와 장축과의 관계
a, b, c 관계 쉽게 암기하는 법
1) 가로로 긴 타원

일단, 제일 중요한건 타원의 정의를 암기하는 것입니다.
그 후에 아래와 같이 중심, 초점, 꼭짓점, 장축, 단축 등을 논하면 됩니다.

또한 c, a, b 사이 관계를 확실히 암기해야 하며,
이에 대한 자세한 내용은 아래에 있습니다.
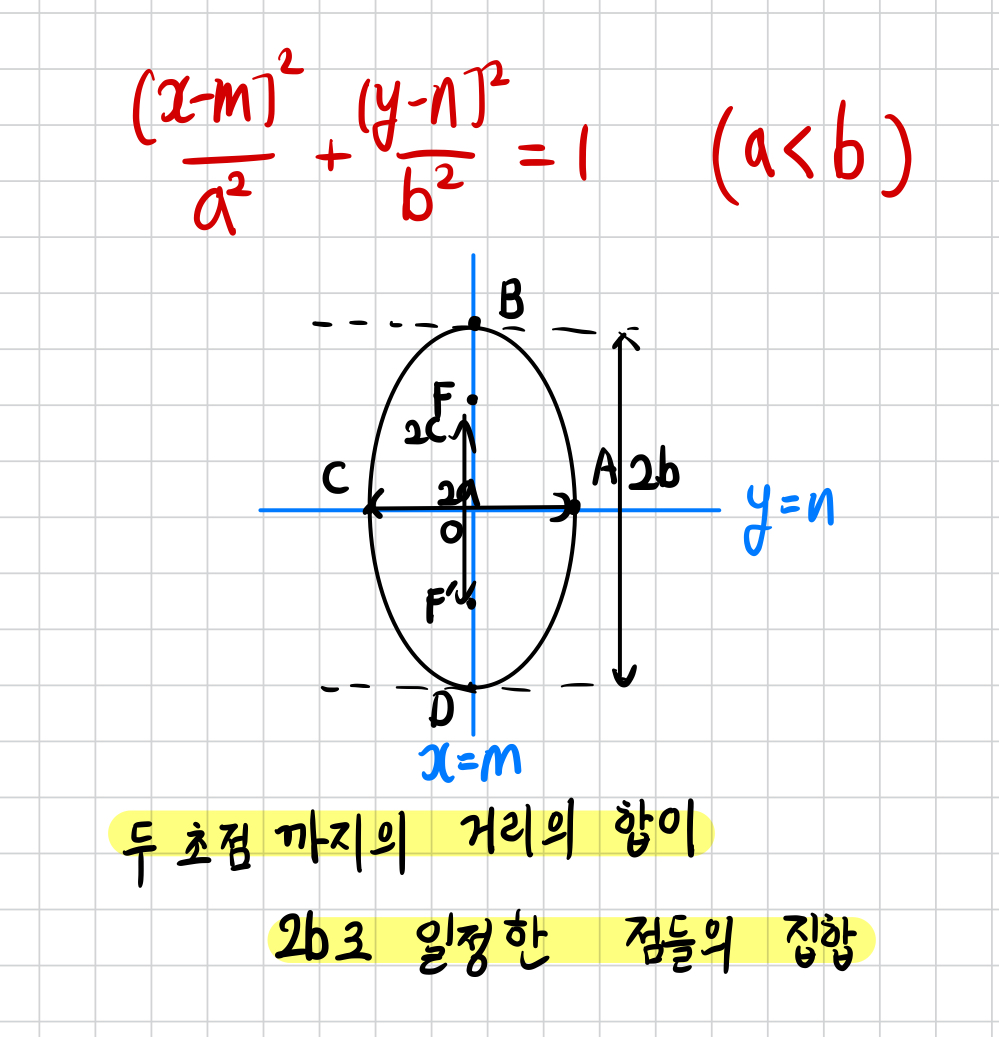
2) 세로로 긴 타원

거리의 합이 2a가 아니라
2b 임에 주의해야 합니다.
마찬가지로 중심, 꼭짓점, 초점, 단축, 장축을 찾을 수 있어야 하고
이때 초점/단축/장축의 값이 아까와 다름에 주의해야 합니다.

a, b, c 관계 또한 아까와 다름에 주목해 주시고
초점 사이의 거리 = 2c 또한 암기해주시면 좋습니다.
자세한 내용은 아래에서 다루겠습니다.
2. 평행이동 형태
평행이동시, 다음과 같은 사실을 받아들여야 합니다.
유지되는 것 : 장축의 길이 / 단축의 길이 / 초점사이 거리 / a, b, c 값
바뀌는 것 : 중심, 초점, 꼭짓점
1) 가로로 긴 타원

2) 세로로 긴 타원
자세한 내용은 아래에서 다루겠습니다.
3. 타원의 정의 활용
앞서 타원의 개형에 대해 공부했지만
결국, 기출에서는 "타원의 정의"를 활용해서 문제를 해결해야 합니다.
따라서 다음과 같이 '정의를 활용하는 마인드셋'을 장착하면 쉽습니다.
1) 타원과 삼각형
2) 타원과 타원
3) 타원과 원
어떤 마인드셋인지는 아래 내용에서 본격적으로같이 공부해 봅시다.
[1] 기본형태
쉬운 내용이긴 하지만
생각할 때 편한 TIP 들을 알려드리곘습니다.
1. 가로로 긴 타원 vs 세로로 긴 타원
두 타원의 비교는 a와 b의 크기만 비교하면 됩니다!
a > b : 가로로 긴 타원 -> *장축의 길이 = 2a
a < b : 세로로 긴 타원 -> *장축의 길이 = 2b
두 타원의 그림은 아래와 같으며
아래 4가지 요소의 차이에 집중하며 학습하면 좋습니다.
정의 / 장축&단축 / 초점의 위치 / a, b, c 관계식

형광펜으로 서로 다른 것을 표시했으니,
확실하게 암기해주시면 공부할 때 편할겁니다!
2. 타원의 정의와 장축과의 관계
가로로 긴 타원을 기준으로 타원의 정의를 생각해봅시다.
'두 초점 까지의 거리의 합이 2a 이다'
위 정의를 타원의 그래프에서 알아낼 수 있는 방법은 없을까요?
HINT : 장축의 길이
즉, 타원의 정의의 거리의 합과 장축의 길이가 일치하는데
과연 우연일까요?
다음 그림을 보시면 확 이해가 될 겁니다.
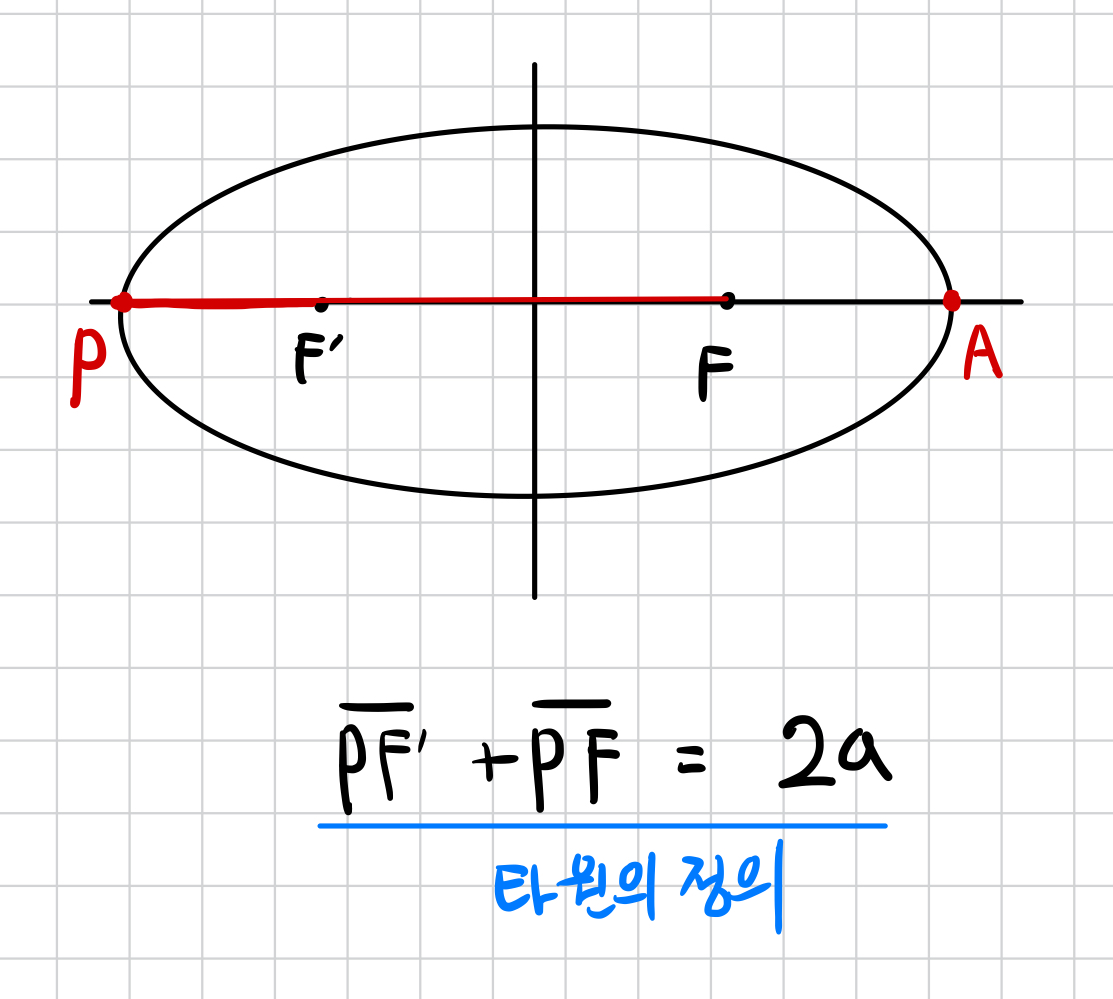
점P에 대하여 타원의 정의를 생각해봅시다.
그러면 PF' + PF = 2a 인 상황입니다.
그런데, PF' = FA 라고 볼 수 있으니 (대칭이니까)
PF'+PF = FA + PF = PA = 장축의 길이
따라서, 장축의 길이 = 2a
라는 사실이 다시한번 확인되게 됩니다.
천천히 생각해보며 그 의미를 발견하시면 좋겠습니다.
3. a, b, c 관계 쉽게 암기하는 법
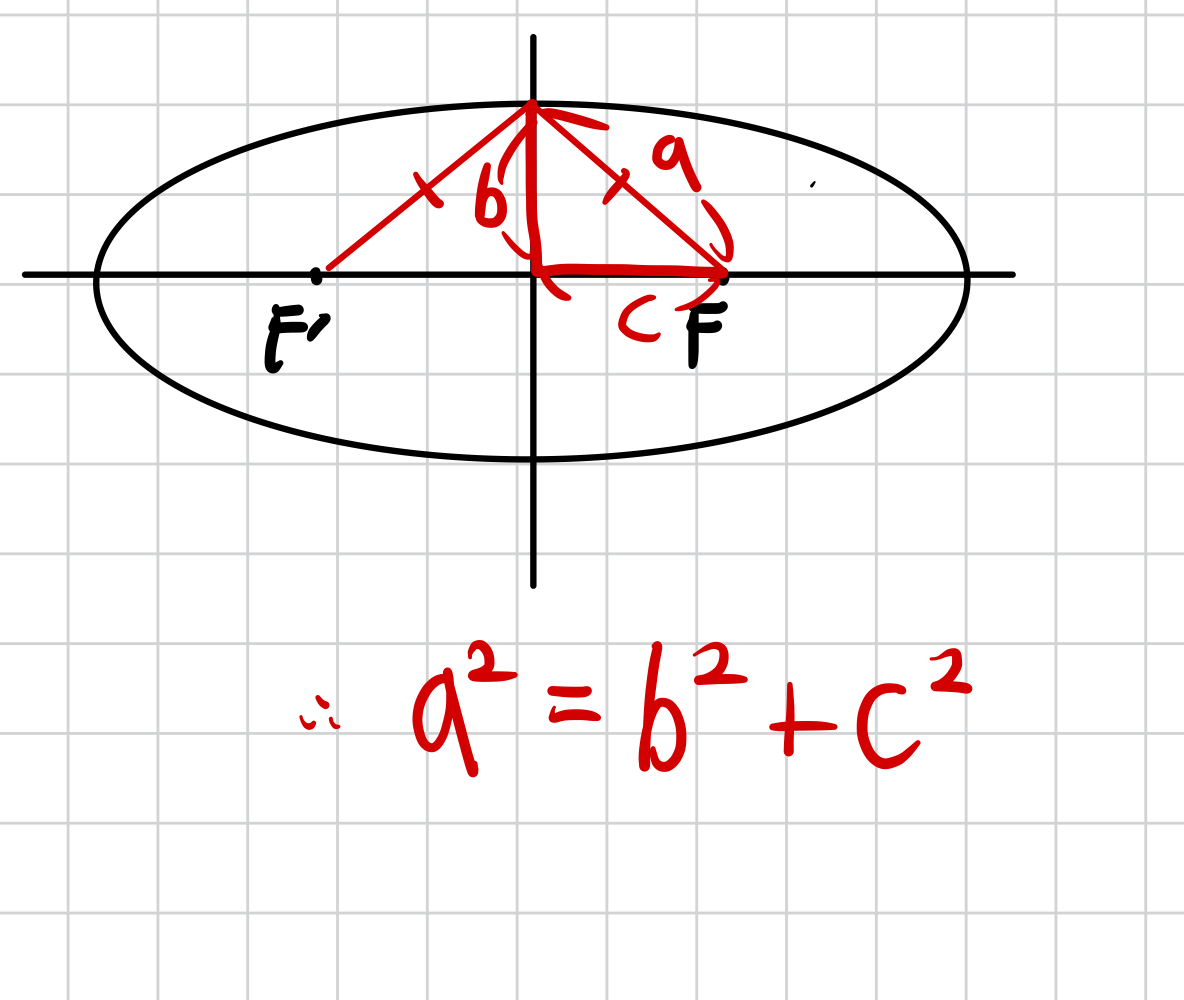
방법1) 직각삼각형 그리기
다음 그림처럼 직각삼각형을 그려서 생각하시면 좋습니다.
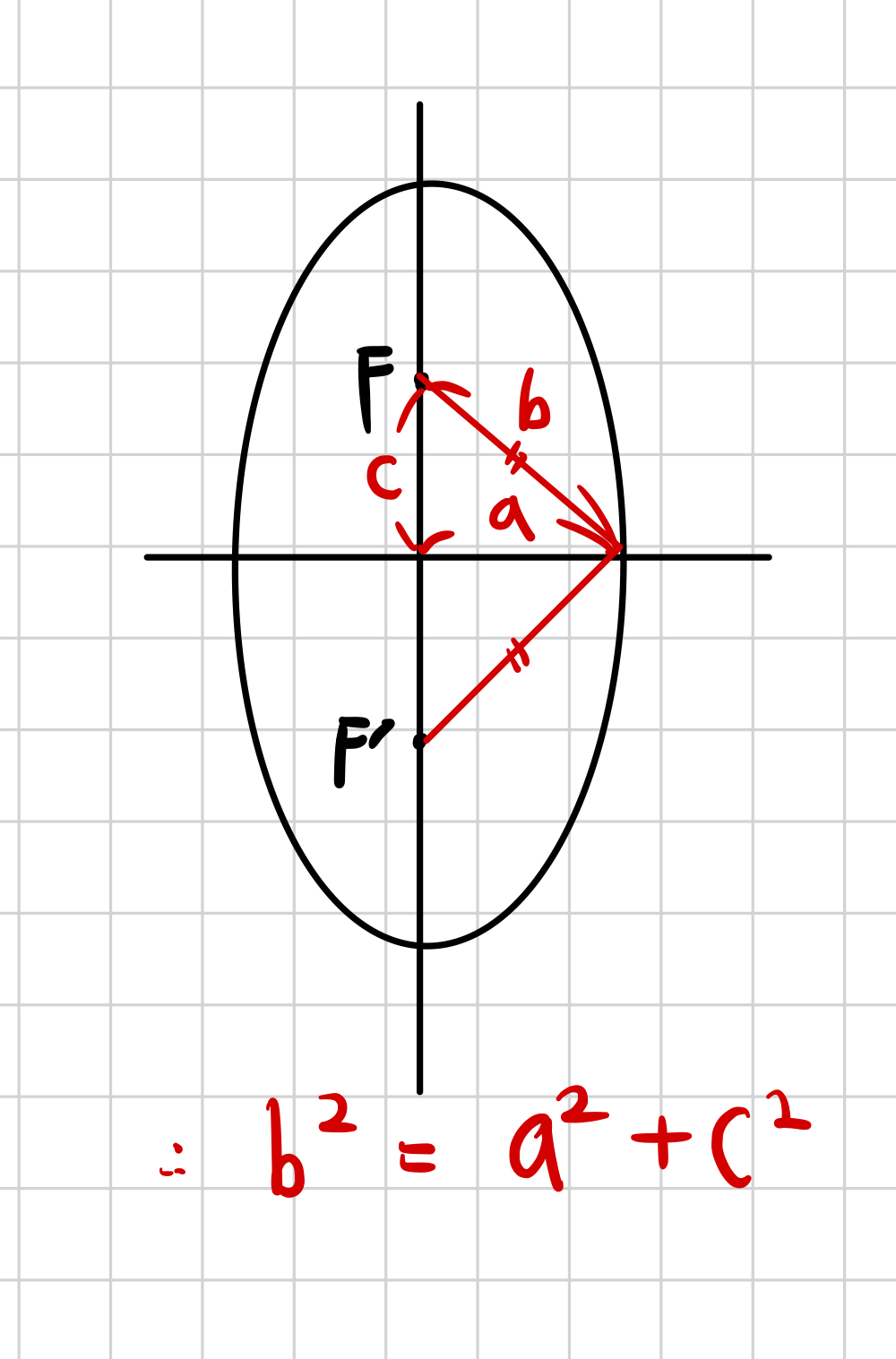
해당 내용은 세로로 긴 타원의 그림도 같이 첨부하겠습니다.
이해되시나요?
특히, 왜 빗변의 길이가 a인지 생각해보시면 좋을듯 합니다.
세로로 긴 타원의 경우는 아래와 같습니다.
방법2) 타원의 방정식에서 c 바로 구하기
큰 값에서 작은 값을 뺀 것 = c제곱
라고 외워두시면 됩니다.
예를 들어 다음과 같은 상황에서 바로 c를 구할 수 있습니다.
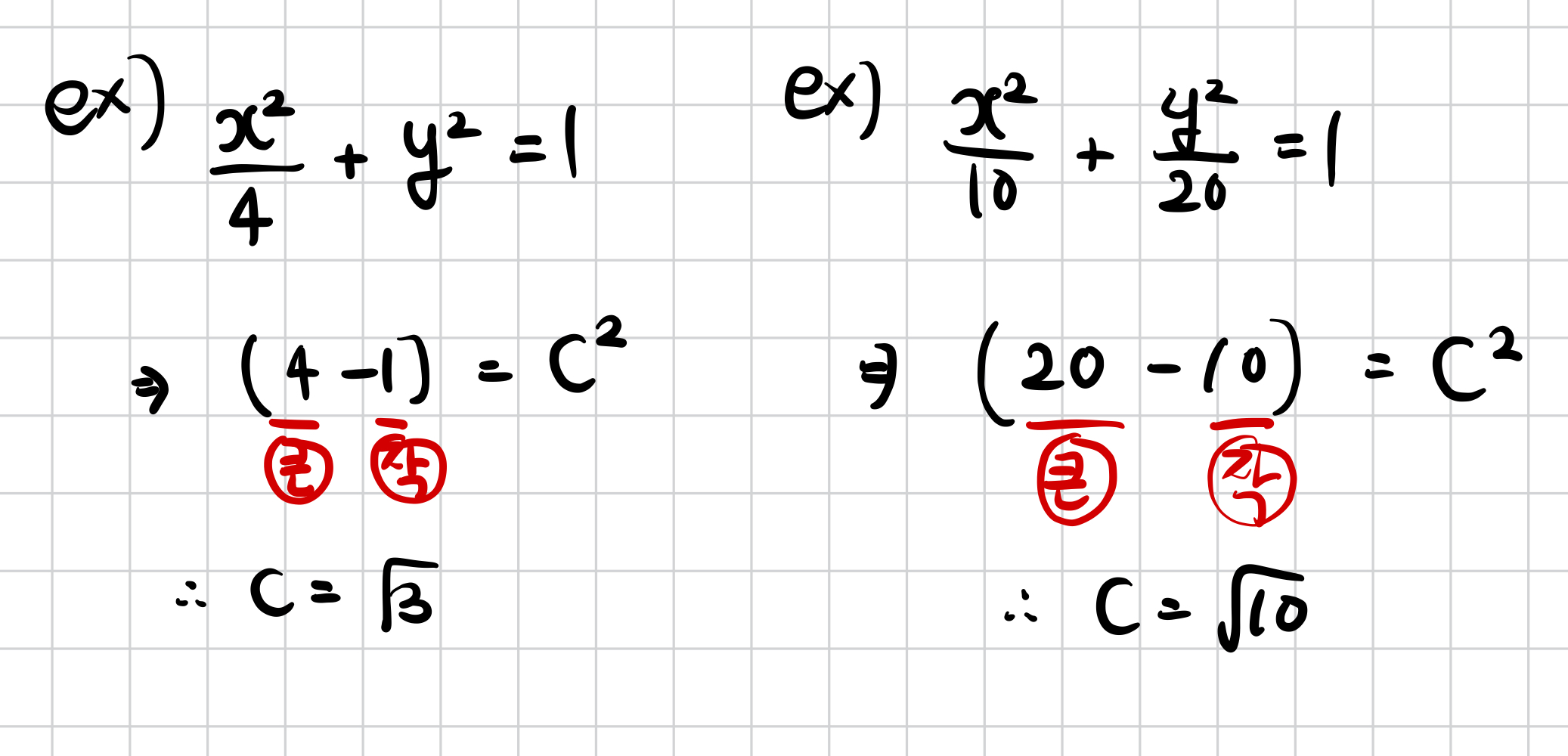
성립하는 이유는 스스로 고민해보시면 좋을 것 같습니다.
쉬운 예제 하나 풀고 다음 내용으로 넘어갑시다.

.
.
.
.
.
직접 풀고
풀이를 봐주세요
.
.
.
.
.
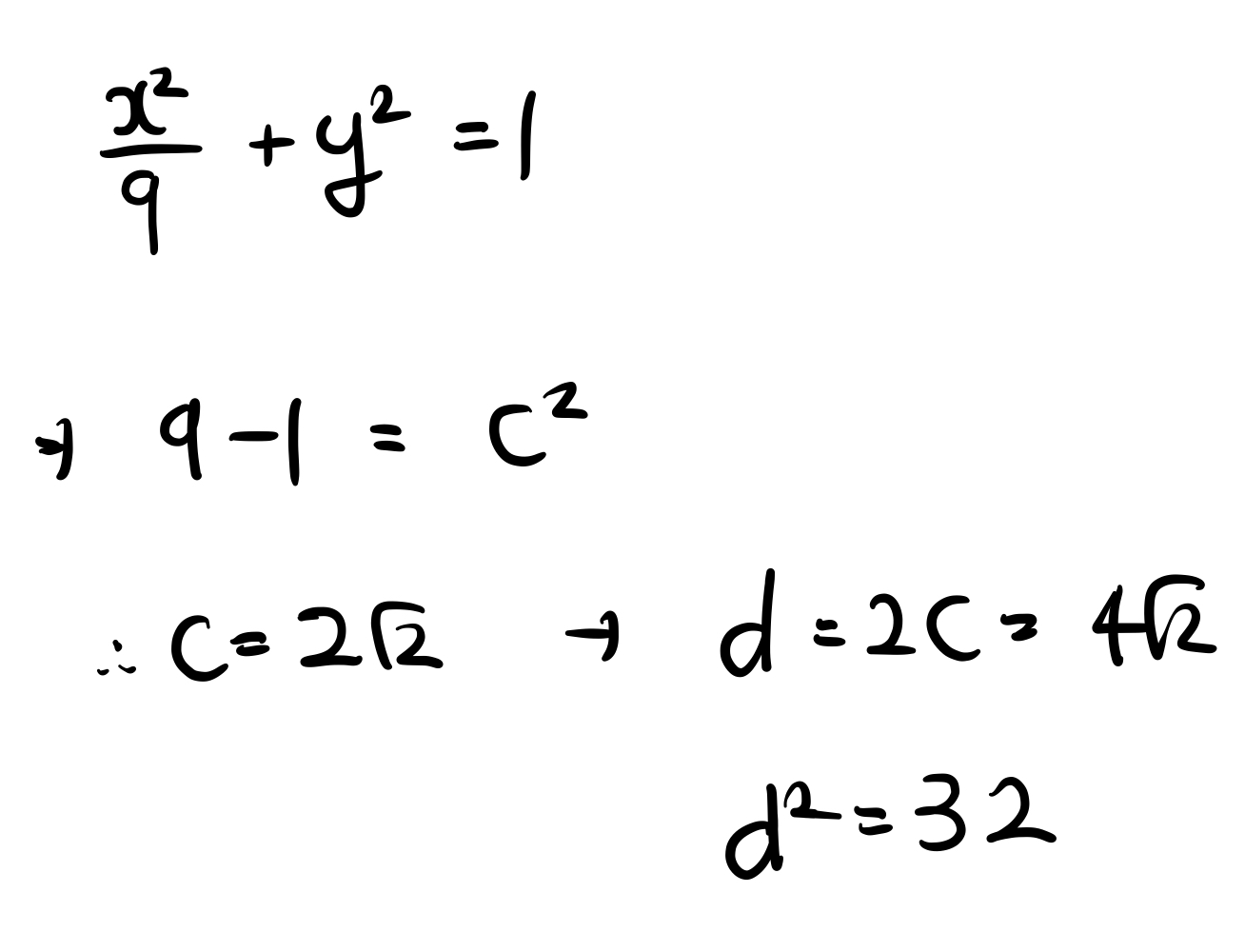
다음 내용으로 갑시다.
[2] 평행이동 된 형태
평행이동 된 타원을 공부할 때
1) 무엇이 바뀌고 무엇이 안바뀌는 지
2) 많은 문제를 풀며 익숙해졌는 지
가 제일 중요하다고 생각하니, 이점에 유의하여 학습합시다.
1. 가로로 긴 타원
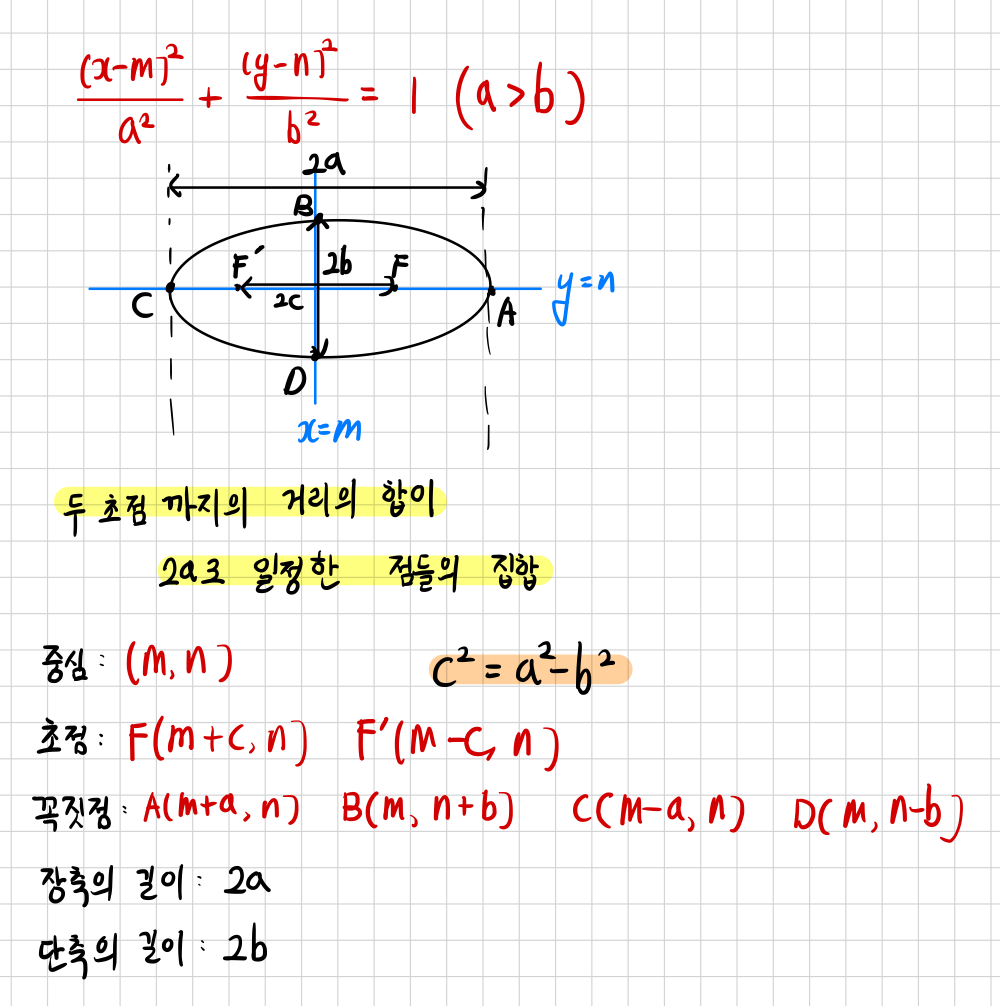
위 그림을 보며
중심 / 초점 / 꼭짓점 / 장축의 길이 / 단축의 길이 / 초점사이 거리
중
무엇이 바뀌고 무엇이 안바뀌는 지
그리고
바뀐다면 얼마나 바뀌는 지 스스로 생각해보시면 좋습니다.
결론적으로, 중심, 초점, 꼭짓점은 (m, n) 만큼 평행이동 되고
장축의 길이, 단축의 길이, 초점사이 거리, a b c 관계식은 유지됩니다.
2. 세로로 긴 타원

세로로 긴 타원의 경우 위 그림과 같으며
앞서 말한 대로 문제를 푸는 것이 중요하기에
같이 연습문제 몇개를 해결해 봅시다.
3. 예제 연습
예제1)

예제2)

예제3)

.
.
.
.
.
직접 풀고
풀이를 봐주세요
.
.
.
.
.


[3] 타원의 정의 활용
타원의 정의 자체는 그리 어려울게 없으나,
정의 활용 문제를 처음 풀때는 꽤 까다로울 수 있습니다.
타원의 정의를 사용하는 여러 상황을 보며 마인드셋을 장착해 봅시다.
이번 내용은 문제 위주로 설명될 예정입니다.
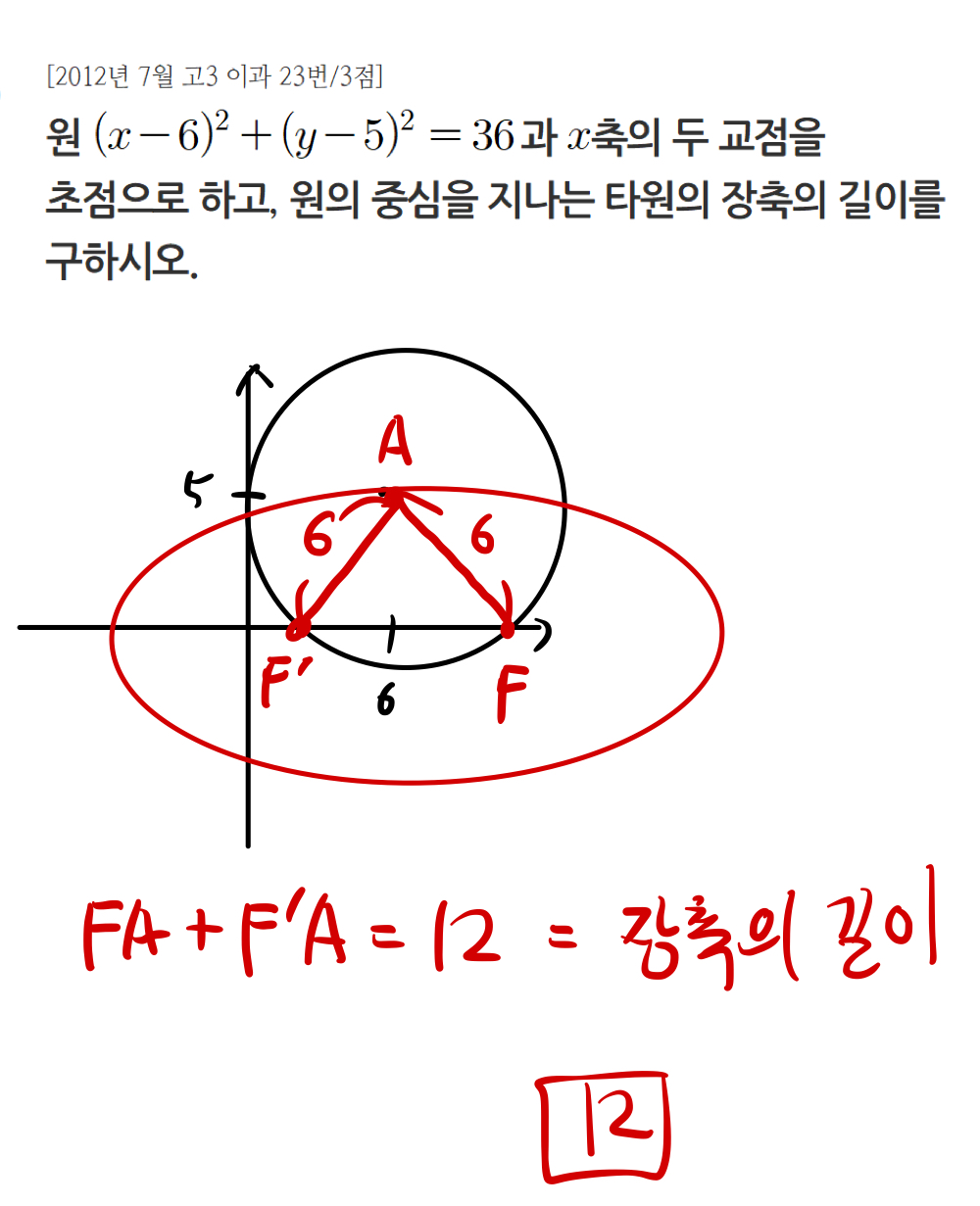
1. 타원과 삼각형

가장 기본적이고 무난한 문제입니다.
직접 타원과 삼각형을 그린 뒤
정의와 엮어서 생각해 보시면 쉽습니다.
.
.
.
.
.
직접 풀고
풀이를 봐주세요
.
.
.
.
.
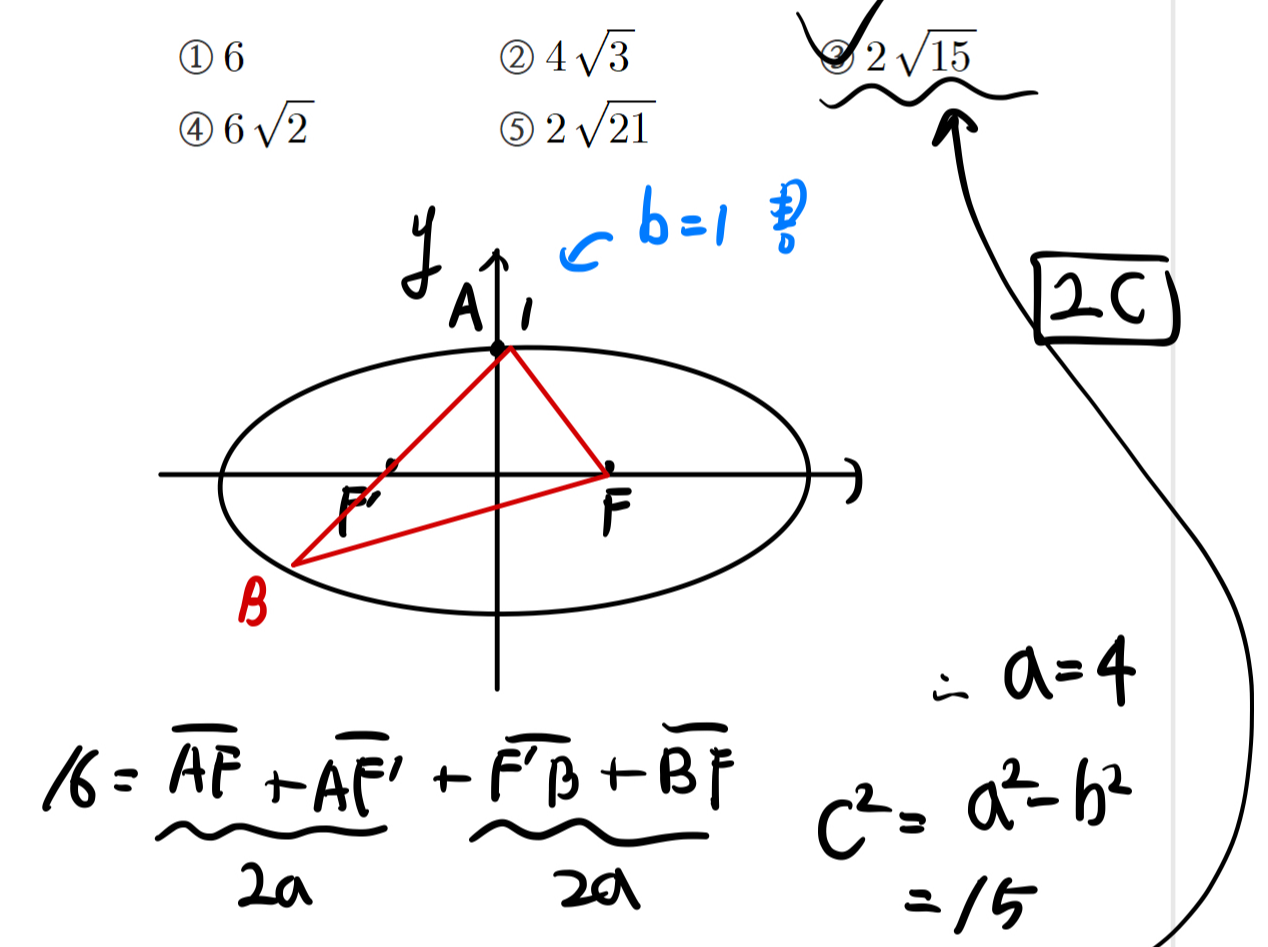
위와 풀이와 같이,
타원의 두 초점을 지나가는 삼각형의 둘레
= 장축의 길이 * 2
라고 생각해두시면 됩니다.
2. 타원과 타원

그리 어렵지 않은 문제이니
스스로 한번 고민해보면 좋을듯 합니다.
.
.
.
.
.
직접 풀고
풀이를 봐주세요
.
.
.
.
.
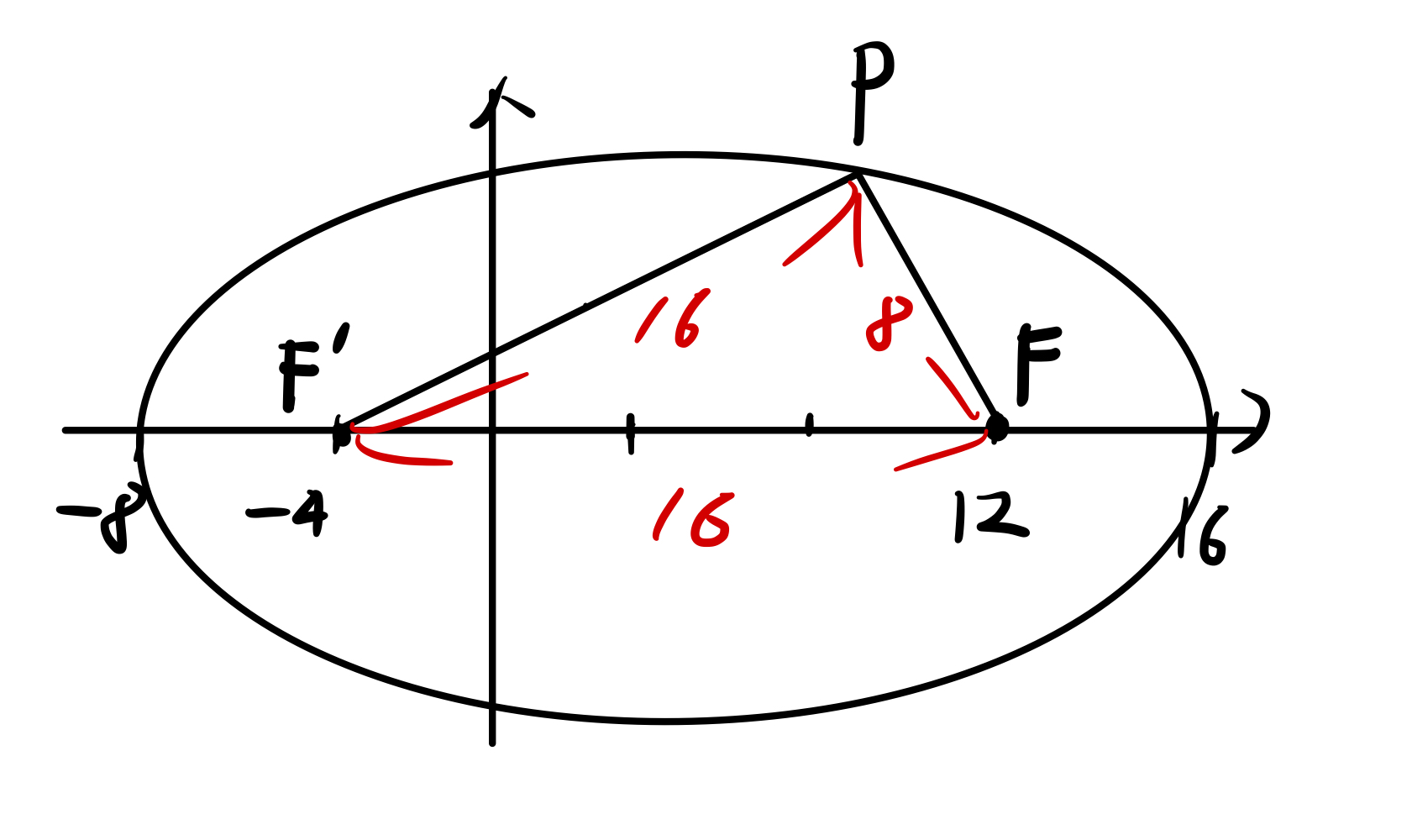
일단 큰 타원과 점 P는 위 그림과 같을 겁니다.
이제 점 Q와 작은 원을 그려보겠습니다.
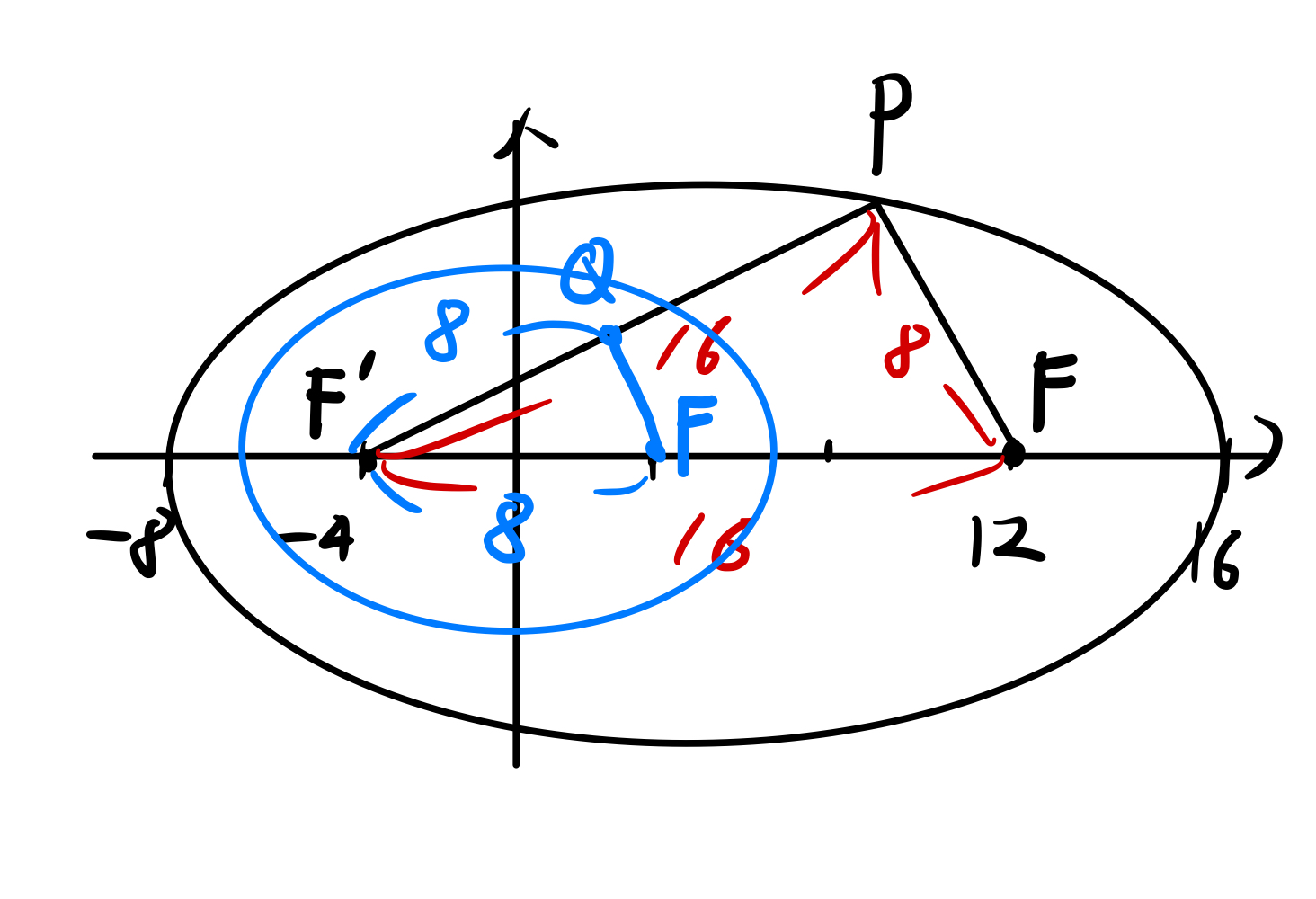
문제 식에서 작은 타원의 중심이 (0, 0) 이므로
작은 타원의 다른 초점은 (4, 0) 이 됩니다.
이때, 삼각형 F'QF(파랑) 와 삼각형 F'PF(검정) 이
서로 닮음비가 1:2 인 삼각형이므로
타원 또한 닮음비가 1:2 임을
직관적으로 이해할 수 있습니다.
그러므로,
2a = 12 -> a = 6
2c = 8 -> c = 4
b^2 = a^2-c^2 = 20
답 : 8 + 36 + 20 = 64
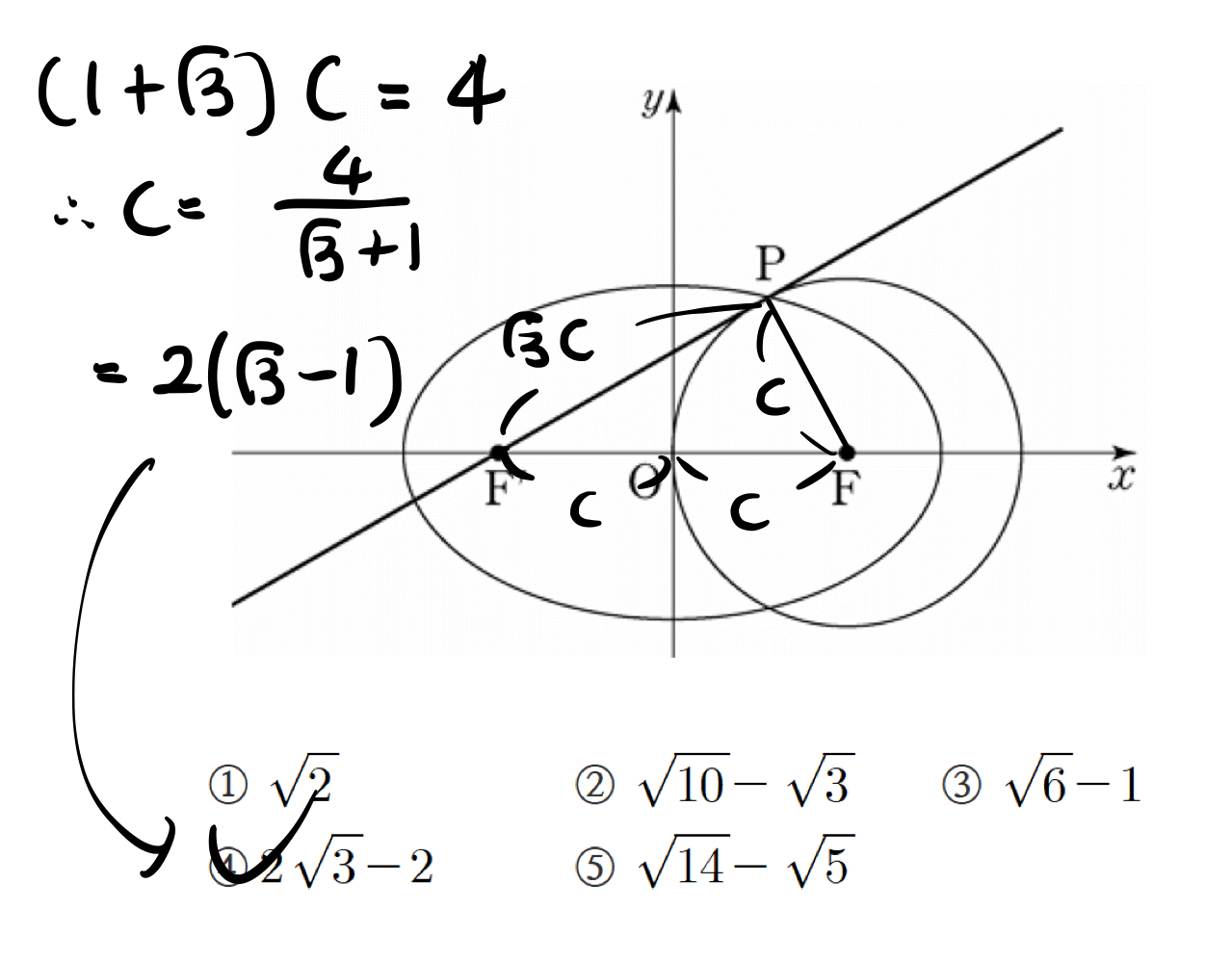
3. 타원과 원

이 문제도 어렵지 않은 편이니, 먼저 풀어보시고
어려운 문제의 경우 문제풀이 영상 강의에서 같이 보면 될 것 같습니다!
.
.
.
.
.
직접 풀고
풀이를 봐주세요
.
.
.
.
.
오늘 5강에서는 타원의 방정식 총정리에 대해 공부했습니다.
다음 5강에서는 타원과 접선에 대해 공부할 예정이며
학습지를 꼭 풀어보신 뒤 유튜브에 있는
해설 영상까지 보셔서 오늘 내용을 체화시키길 권장드립니다!
개념 영상 링크 : https://youtu.be/ffpAsvMXiWA
해설 영상 링크 : https://youtu.be/2dJntkMmRZk
그럼 다음 강의에서 뵙겠습니다. 화이팅!
'밤샘수학 > 기하 실전 개념' 카테고리의 다른 글
| [기하 실전 개념 6강] 타원의 접선 총정리 (1) | 2024.10.03 |
|---|---|
| [기하 실전 개념 4강] 포물선과 접선 총 정리 (4) | 2024.09.28 |
| [기하 실전개념 학습지 파일 정리] (0) | 2024.09.25 |
댓글
이 글 공유하기
다른 글
-
[기하 실전 개념 6강] 타원의 접선 총정리
[기하 실전 개념 6강] 타원의 접선 총정리
2024.10.03 -
[기하 실전 개념 4강] 포물선과 접선 총 정리
[기하 실전 개념 4강] 포물선과 접선 총 정리
2024.09.28 -
[기하 실전개념 학습지 파일 정리]
[기하 실전개념 학습지 파일 정리]
2024.09.25