현대 물리 4강 : 플랑크 흑체 복사 이론
반응형
저번 시간에는 레일리 - 진스의 법칙에 대해 알아보았다.
잠시 정리하자면
레일리 - 진스의 법칙의 경우 파장이 긴 영역에서는 실험 결과 그래프와 비슷한 양상을 띄었으나
파장이 짧은 영역에서는 무한대로 발산하여 실험결과와 차이를 보였다.
따라서 이를 해결하기 위한 인물이 플랑크였는데
플랑크는 흑체 공동에서의 복사가 공동의 벽 내부 원자의 진동에 의한 것으로 여기고 다음 두 가지 가정을 했다.
1. 진동자의 에너지는 양자화 되어 있다.
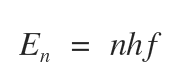
2. 진동자는 한 양자 상태에서 다른 양자 상태로 전이 할 때 에너지를 흡수하거나 방출한다.
또한 플랑크는 에너지 상태에 대해 점유율을 주었다.
즉 에너지가 E인 어떤 상태가 점유될 확률은

에 비례한다.
이를 이용하여 얻은 플랑크 식은 아래와 같다.

여기서 h는 플랑크 상수로서 전 파장에 대해 이론과 실험이 잘 맞도록 도입한 상수이다.
위식은 파장이 큰 영역에서는 레일리 - 진스 식과 같아지고
파장이 짧은 영역에서는 지수 함수적으로 감소하여 실험 결과와도 일치한다.
다음시간에는 지금까지 배운 것들을 총정리하고 문제를 몇가지 풀어보자.
반응형
'밤샘물리 > 현대 물리' 카테고리의 다른 글
| 현대 물리 6강 : 광전효과 - 일함수 (0) | 2020.08.27 |
|---|---|
| 현대 물리 5강 : 흑체 복사 총정리 및 문제 풀이 (0) | 2020.08.27 |
| 현대 물리 3강 : 레일리 진스의 법칙(Rayleigh-Jeans law) (0) | 2020.08.27 |
| 현대 물리 2강 : 빈의 변위 법칙 (0) | 2020.08.27 |
| 현대 물리 1강 : 흑체복사와 슈테판 법칙 (0) | 2020.08.26 |
댓글
이 글 공유하기
다른 글
-
현대 물리 6강 : 광전효과 - 일함수
현대 물리 6강 : 광전효과 - 일함수
2020.08.27 -
현대 물리 5강 : 흑체 복사 총정리 및 문제 풀이
현대 물리 5강 : 흑체 복사 총정리 및 문제 풀이
2020.08.27 -
현대 물리 3강 : 레일리 진스의 법칙(Rayleigh-Jeans law)
현대 물리 3강 : 레일리 진스의 법칙(Rayleigh-Jeans law)
2020.08.27 -
현대 물리 2강 : 빈의 변위 법칙
현대 물리 2강 : 빈의 변위 법칙
2020.08.27