선형대수학 1강 <행렬의 정의와 연산>

안녕하세요.
오늘은 선형대수학 1강. 행렬의 정의와 연산에 대해 알아봅시다.
가독성을 위해 평어체로 쓰도록 하겠습니다.
목차부터 봅시다.
1강 <행렬의 정의와 연산> 목차
1. 행렬의 정의
(1) 행렬의 기초
① 행과 열의 구분
② 정사각행렬과 대각성분
③ 행렬의 상등 (같은 행렬)
2. 행렬의 덧셈과 뺄셈
(1) 항등원과 역원의 정의
① 항등원의 정의
② 역원의 정의
③ 정리
(2) 행렬의 실수배와 덧셈
① 행렬의 실수배의 정의
② 행렬의 덧셈의 정의
(3) 행렬의 실수배와 덧셈에 대한 성질
① 성질1. 교환법칙
② 성질2. 결합법칙
③ 성질3. 항등원
④ 성질4. 역원
⑤ 성질5. 기타
⑥ 성질 정리
3. 행렬의 곱셈과 정칙행렬
(1) 행렬의 곱셈
① 행렬의 곱셈의 정의
② 예시
(2) 행렬의 곱셈에 대한 성질
① 성질1. 결합법칙
② 성질2. 분배법칙
③ 성질3. 실수배
④ 성질4. 영행렬
⑤ 성질5. 항등원
⑥ 성질 정리
(3) 정칙행렬과 정칙행렬에 대한 성질
① 정칙행렬의 정의
② 성질1. 역행렬의 유일성
③ 성질2. 역행렬의 역행렬
④ 성질3. 정칙행렬의 거듭제곱
⑤ 성질4. 정칙행렬의 실수배
⑥ 성질5. 정칙행렬의 곱셈
⑦ 성질 정리
1. 행렬의 정의
(1) 행렬의 기초
① '행'과 '열'의 구분

선형대수학을 처음 배우다 보면 행(row)과 열(column)을 혼동하는 경우가 있는데 비'행'기와 '열'기구로 외우면 편하다. (* 비'행'기는 가로로 날고, '열'기구는 세로로 날기 때문)
② 정사각행렬과 대각성분
또한 mxn 행렬(matrix)라고 하면 행이 m개, 열이 n개인 크기의 행렬을 의미한다.
특히, nxn 행렬을 n 차의 정사각행렬이라 하며 성분 a11, a22, ... , ann을 A의 대각성분이라고 한다.

(* 즉, 대각성분은 정사각행렬에서만 정의된다.)
③ 행렬의 상등 (같은 행렬)
크기가 같은 두 행렬 A, B에 대하여 모든 원소가 같을때 두 행렬을 같은행렬이라 하며 A = B 로 표기한다.

2. 행렬의 덧셈과 뺄셈
(1) 항등원과 역원의 정의
① 항등원의 정의
항등원은 "임의의 수에 특정 연산을 했을 때 자기 자신이 되도록 하는 수"를 말한다.
(*이해를 돕기 위해 편의상 임의의 수라고 했으나 정확히는 임의의 원소[실수, 다항식, 행렬, 벡터 등]로 정의해야 올바르다)

예를들어,
실수의 덧셈에서, 덧셈의 항등원은 0이다. (0을 더하면 자기자신 이므로)
실수의 곱셈에서, 곱셈의 항등원은 1이다. (1을 곱하면 자기자신 이므로)
함수의 합성에서, 합성의 항등원은 항등함수이다. (항등함수를 합성하면 자기자신 이므로)

② 역원의 정의
역원은 "임의의 수에 특정 연산을 했을 때 항등원이 되도록 하는 "를 말한다.
(*이해를 돕기 위해 편의상 임의의 수라고 했으나 정확히는 임의의 원소[실수, 다항식, 행렬, 벡터 등]로 정의해야 올바르다)

예를들어,
실수의 덧셈에서, 덧셈의 역원은 -A 이다. (임의의 A에 -A를 더하면 0 이므로)
실수의 곱셈에서, 곱셈의 역원은 1/A이다. (임의의 A에 1/A를 곱하면 1 이므로)
함수의 합성에서, 합성의 역원은 역함수이다. (임의의 함수에 역함수를 합성하면 항등함수 이므로)

③ 정리
| 집합 | 연산자 | 항등원 | 역원 |
| 실수 | 덧셈 | 0 | -A |
| 곱셈 | 1 | 1/A | |
| 정사각 행렬 | 덧셈 | 0행렬 | -A |
| 곱셈 | 항등행렬 | 역행렬 |
(*정사각행렬의 항등원과 역원은 뒤에서 자세히 다룰 것이므로, 지금은 그냥 넘어가도 됨)
(2) 행렬의 실수배와 덧셈
① 행렬의 실수배의 정의
행렬의 실수배는 각 원소를 말 그대로 실수배한 행렬이 나온다고 생각하면 쉽다.
예를들어 다음과 같이 2A를 생각할 수 있다.
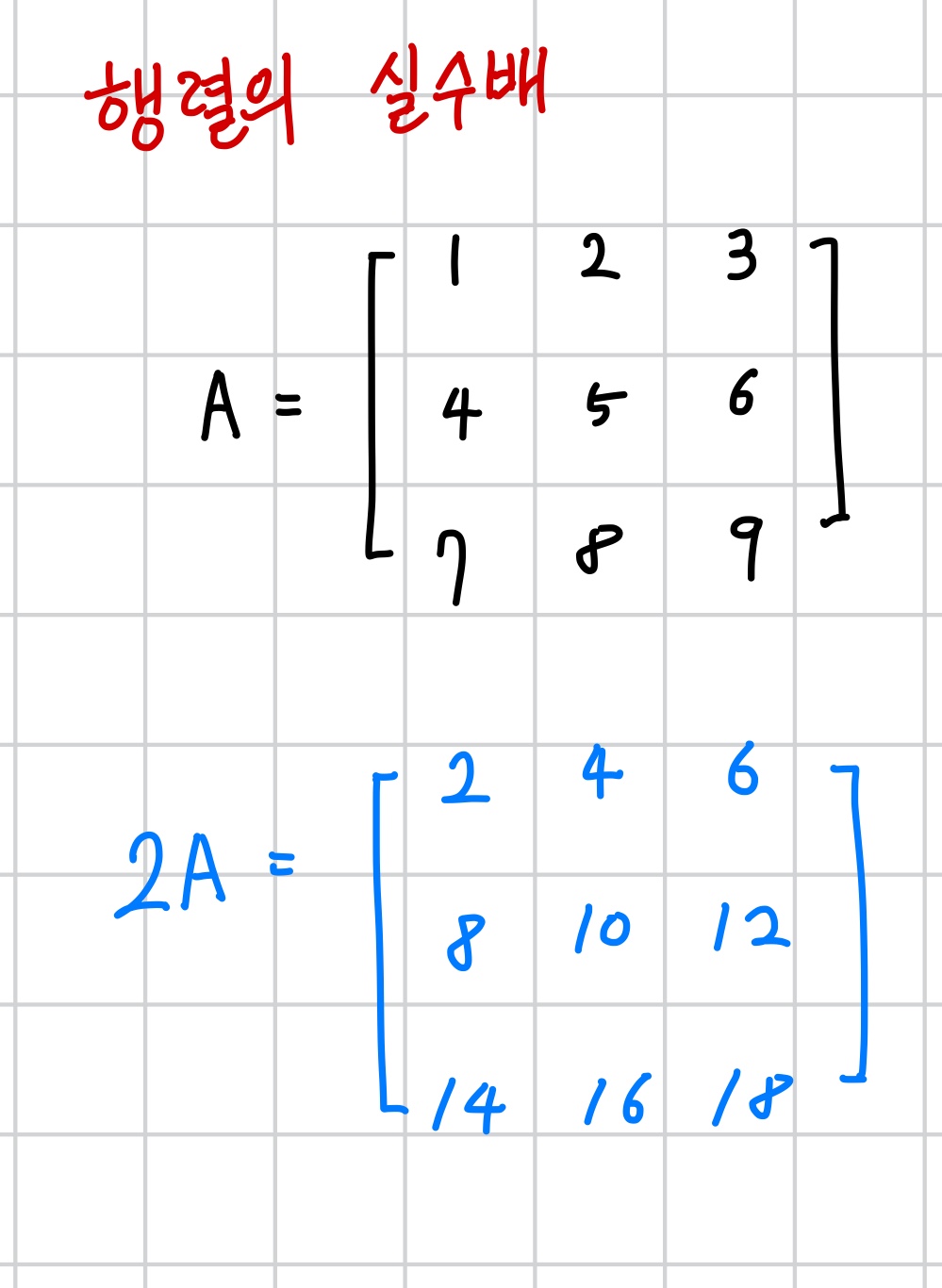
② 행렬의 덧셈의 정의
행렬의 덧셈은 같은 크기의 두 행렬에서 각각의 원소를 합친 결과를 원소로하는 행렬이 나온다고 생각하면 쉽다.
예를들어 다음과 같이 A+B를 생각할 수 있다.

(3) 행렬의 실수배와 덧셈에 대한 성질
① 성질1. 교환법칙

증명)
② 성질2. 결합법칙

증명) 생략
③ 성질3. 항등원

증명) 생략
④ 성질4. 역원

증명) 생략
⑤ 성질5. 기타

증명) 생략
⑥ 성질 정리
성질1. 행렬의 덧셈은 교환법칙이 성립한다.
성질2. 행렬의 덧셈은 결합법칙이 성립한다.
성질3. 행렬의 덧셈의 항등원은 0행렬이다.
성질4. 행렬의 덧셈의 역원은 -A이다.
성질5. 행렬의 실수배에 대한 다양한 성질이 성립한다.
3. 행렬의 곱셈과 정칙행렬
(1) 행렬의 곱셈
① 행렬의 곱셈의 정의
행렬의 곱셈은 실수의 곱셈과 달리 매우 복잡한 계산을 거친다.
또한, 행렬의 곱셈은 임의의 두 행렬에 대하여 항상 성립하는 연산이 아니며 행렬의 크기가 잘 맞아야 한다.

(2x4 행렬과 4x3 행렬의 곱은 2x3 행렬이 나오지만, 2x4 행렬과 3x4 행렬의 곱은 애초에 정의되지 않는다)
A X B = C 라 할때, C의 i행j열 성분의 값은 A의 i행 성분들과 B의 j행 성분들 각각의 곱의 합이 된다.
② 예시
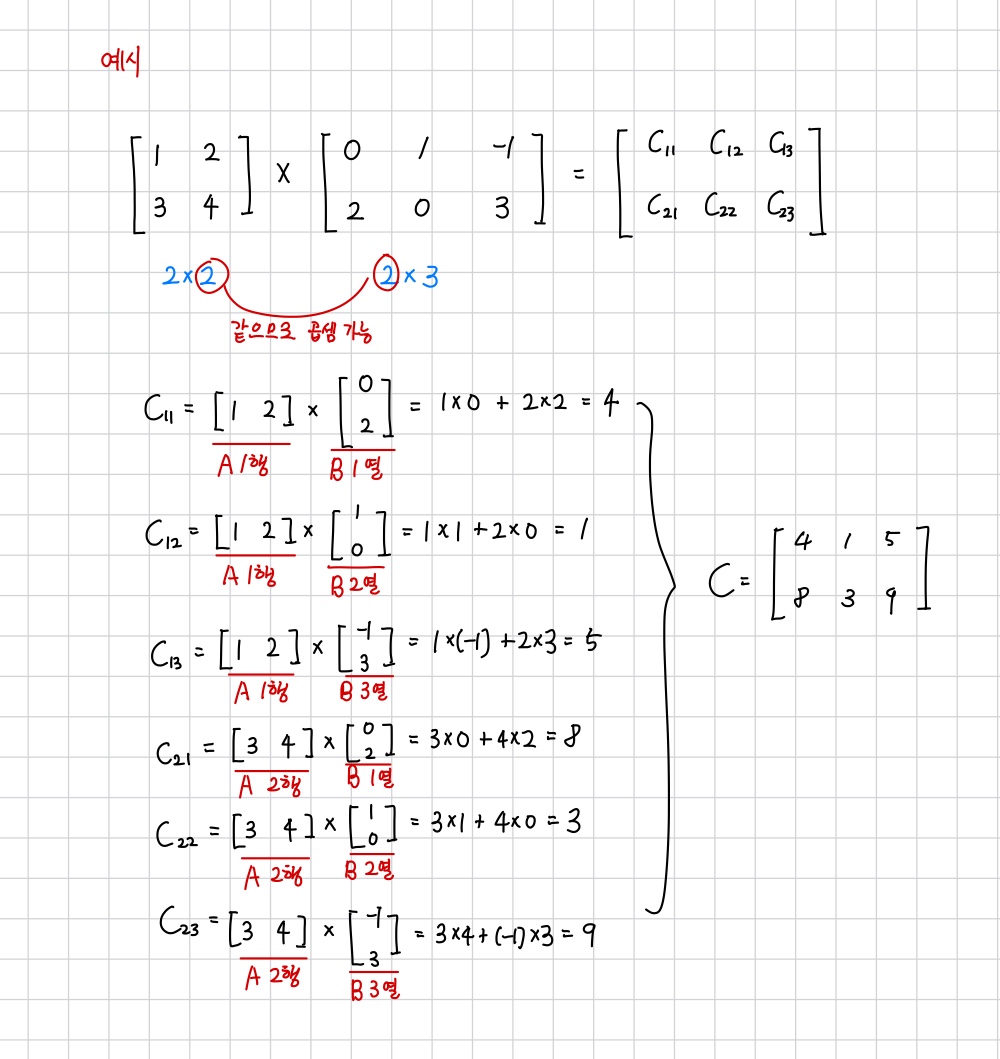
(2) 행렬의 곱셈에 대한 성질
① 성질1. 결합법칙

증명) 생략
② 성질2. 분배법칙

증명) 생략
③ 성질3. 실수배와 결합법칙

증명) 생략
④ 성질4. 영행렬
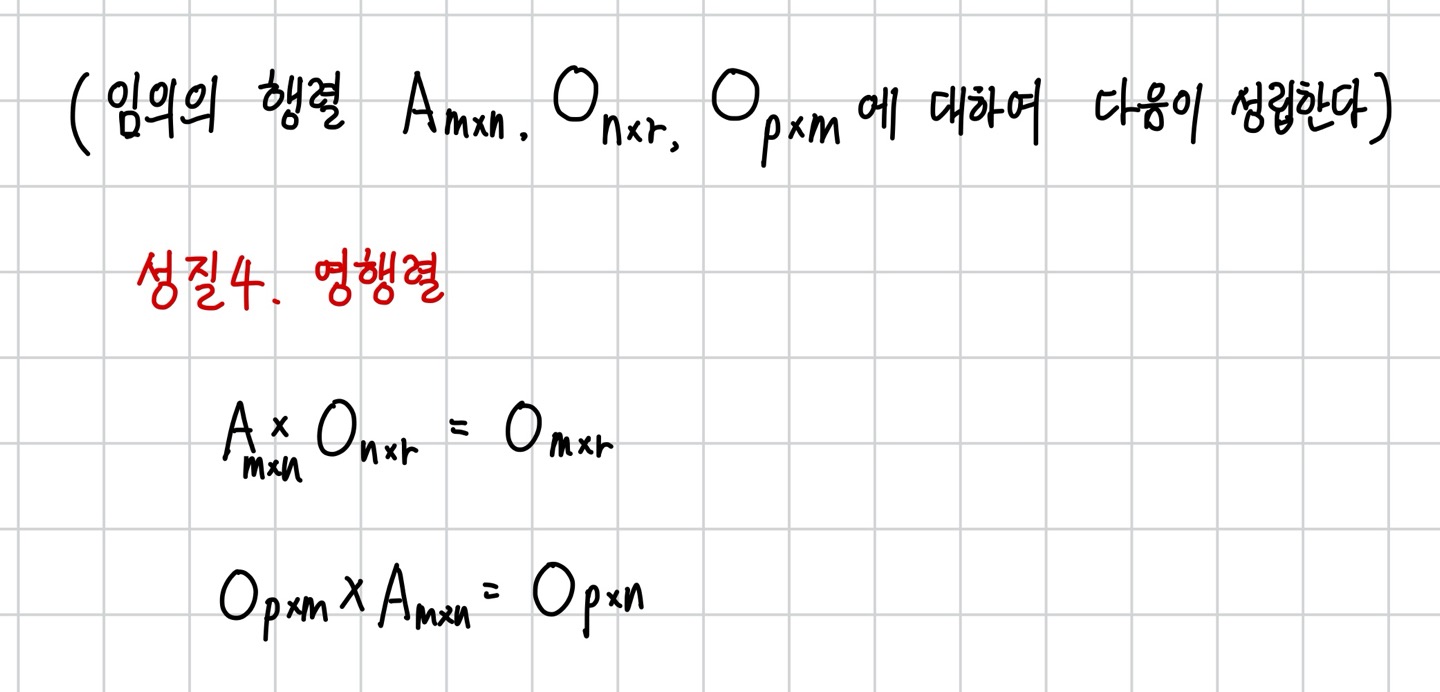
증명) 생략
⑤ 성질5. 항등원

증명) 생략
⑥ 성질 정리
성질1. 행렬의 곱셈은 결합법칙이 성립한다.
성질2. 행렬의 곱셈은 분배법칙이 성립한다.
성질3. 행렬의 곱셉은 실수배와 관련된 결합법칙이 성립한다.
성질4. 행렬의 곱셈에서 0행렬을 곱하면 0행렬이 나온다.
성질5. 행렬의 곱셈의 항등원은 항등행렬이다.
(3) 정칙행렬과 정칙행렬에 대한 성질
① 정칙행렬의 정의

정칙행렬은 정사각행렬 A에 대하여, A가 곱셈에 대한 역원이 존재할때 A를 정칙행렬 또는 가역행렬이라 한다.
또한, 이때 A의 곱셈에 대한 역원인 행렬 B를 A의 역행렬이라고 하며 A^(-1) 로 나타낸다.
(*정칙행렬은 정사각행렬에서 정의된다)
(**즉, 모든 정사각행렬이 역행렬을 가지는 것은 아니다 = 모든 정사각행렬이 정칙행렬인 것은 아니다)
② 성질1. 역행렬의 유일성

증명) 생략
③ 성질2. 역행렬의 역행렬

증명) 생략
④ 성질3. 정칙행렬의 거듭제곱

증명) 생략
⑤ 성질4. 정칙행렬의 실수배

증명) 생략
⑥ 성질5. 정칙행렬의 곱셈

증명) 생략
⑦ 성질 정리
성질1. 정칙행렬 A에 대하여, A^(-1)은 유일하다.
성질2. 정칙행렬 A에 대하여, [A^(-1)]^(-1) = A 이다.
성질3. 정칙행렬 A에 대하여, (A^n)^(-1) = [A^(-1)]^n 이다.
성질4. 정칙행렬 A에 대하여, (kA)^(-1) = 1/k x A^(-1) 이다.
성질5. 정칙행렬 A, B에 대하여, (A x B)^(-1) = B^(-1) x A^(-1) 이다.
양이 좀 많긴 하지만 ㅎㅎ,,
선형대수학 1강. 행렬의 정의와 연산에 대해 정리해 보았습니다.
다음 목차를 보며 다시 한번 배운 내용을 상기시켜보면 좋을 것 같습니다.
1. 행렬의 정의
(1) 행렬의 기초
① 행과 열의 구분
② 정사각행렬과 대각성분
③ 행렬의 상등 (같은 행렬)
2. 행렬의 덧셈과 뺄셈
(1) 항등원과 역원의 정의
① 항등원의 정의
② 역원의 정의
③ 정리
(2) 행렬의 실수배와 덧셈
① 행렬의 실수배의 정의
② 행렬의 덧셈의 정의
(3) 행렬의 실수배와 덧셈에 대한 성질
① 성질1. 교환법칙
② 성질2. 결합법칙
③ 성질3. 항등원
④ 성질4. 역원
⑤ 성질5. 기타
⑥ 성질 정리
3. 행렬의 곱셈과 정칙행렬
(1) 행렬의 곱셈
① 행렬의 곱셈의 정의
② 예시
(2) 행렬의 곱셈에 대한 성질
① 성질1. 결합법칙
② 성질2. 분배법칙
③ 성질3. 실수배
④ 성질4. 영행렬
⑤ 성질5. 항등원
⑥ 성질 정리
(3) 정칙행렬과 정칙행렬에 대한 성질
① 정칙행렬의 정의
② 성질1. 역행렬의 유일성
③ 성질2. 역행렬의 역행렬
④ 성질3. 정칙행렬의 거듭제곱
⑤ 성질4. 정칙행렬의 실수배
⑥ 성질5. 정칙행렬의 곱셈
⑦ 성질 정리
다음시간에는 선형대수학 2강. 특별한 행렬에 대해 공부하도록 하겠습니다~
'밤샘수학 > 선형대수학 (Linear Algebra)' 카테고리의 다른 글
| 선형대수학 0강 <목차> (0) | 2024.03.29 |
|---|